大家好,小师妹又和大家见面啦。在了解完贝叶斯网络相关的基础知识后,同学们是不是已经跃跃欲试了?那么就让我们从一个较为简单的例子开始吧!

在本例中,小师妹将带大家使用R语言bnlearn包中附带的learning.test数据集,该数据集是由共6个从属分类分布的节点构成,也就是说每个节点都隶属于一个离散分布:
library(bnlearn)data(learning.test)summary(learning.test)
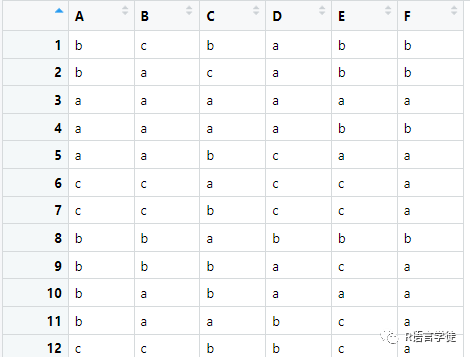
> summary(learning.test)
A B C D E F
a:1668 a:2362 a:3717 a:1755 a:1941 a:2509
b:1670 b: 568 b:1024 b:1570 b:1493 b:2491
c:1662 c:2070 c: 259 c:1675 c:1566
接着,小师妹将使用bnlearn中的iamb函数调用iamb方法进行贝叶斯网络结构的学习,让小师妹向大家简单地介绍一下该iamb方法:
“iamb” 是 “Inclusion of Ancestral Nodes via Markov Blanket”(通过马尔科夫毯覆盖包含祖先节点)的缩写,是贝叶斯网络构建中的一种方法。它用于在给定数据集的情况下,通过识别变量的马尔科夫毯来估计变量之间的概率关系。

“iamb” 方法的步骤如下:
- 初始阶段:将每个节点视为一个独立的网络。
- 搜索阶段:对于每个节点,搜索与之关联的节点,形成一个候选的马尔科夫毯。搜索的过程可以使用一些启发式算法,例如遍历邻居节点、计算条件独立性测试等。
- 剪枝阶段:通过条件独立性测试来排除一些不符合条件的节点,从而减小马尔科夫毯的规模。
- 合并阶段:将剩余的节点合并到当前节点的马尔科夫毯中,形成更大的马尔科夫毯。
- 重复步骤:重复以上步骤,直到无法再添加新的节点为止。
通过这个方法,可以逐步识别出每个节点的马尔科夫毯,从而建立贝叶斯网络的结构。这个方法的优点在于,它可以在给定数据集的情况下,通过一些统计测试来推断变量之间的条件独立性,从而帮助确定网络结构。然而,这个方法也可能受到数据噪音和采样量的限制。在实际应用中,通常需要结合领域知识和其他算法来完善贝叶斯网络的构建。
初学的小伙伴们看到这里可能就开始担心了,那么怎么运用R语言通过已知数据调用iamb方法构建贝叶斯网络呢?小师妹说,只需一行代码!
pdag = iamb(learning.test)
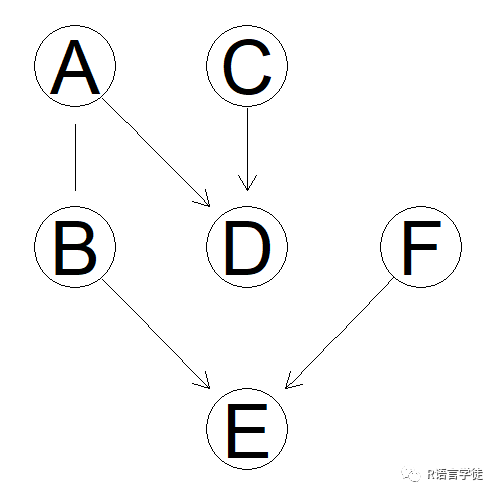
初学的小伙伴们,只需调用bnlearn中的iamb函数,并将给定的数据集作为输入,就完成贝叶斯网络的简单构建啦,是不是非常简单呢?让我们看看由该函数创建的贝叶斯网络是什么样:
pdagpp = graphviz.plot(pdag)
> pdag
Bayesian network learned via Constraint-based methods
model: [partially directed graph] nodes: 6 arcs: 5 undirected arcs: 1 directed arcs: 4 average markov blanket size: 2.33 average neighbourhood size: 1.67 average branching factor: 0.67
learning algorithm: IAMB conditional independence test: Mutual Information (disc.) alpha threshold: 0.05 tests used in the learning procedure: 134 细心的小伙伴们可能发现了,节点A和节点B之间的弧并非标准的有向弧,而是一种无向弧,这又是为什么呢?我们调用score()函数去计算节点A、B之间的BDe得分。
score 函数用于计算贝叶斯网络的分数,帮助评估网络结构的拟合程度,从而可以用来比较不同网络结构之间的好坏。贝叶斯网络的分数通常基于数据拟合程度和模型复杂度两个因素。具体地,score 函数的原理是通过一个损失函数来衡量数据拟合程度和模型复杂度之间的权衡。常用的损失函数之一是 BDe(Bayesian Dirichlet equivalence),它考虑了变量之间的条件概率分布以及网络的结构。
其中: LL 表示对数似然(Log Likelihood),衡量了模型对观测数据的拟合程度。似然越高,模型越能够解释数据。 |P| 是模型中的参数数量,也就是网络中所有的条件概率分布的参数数量之和。 N 是样本数据的大小。
LL 的计算涉及到观测数据和网络结构,通过计算节点条件概率分布和观测数据的差异来判断数据拟合程度。|P| 越大,模型的复杂度越高,而 log(N) 则是用来惩罚模型复杂度的项,以防止过度拟合。通过计算 BDe 分数,score 函数可以帮助你比较不同网络结构之间的好坏,选择最适合数据的网络结构。
#计算A to B和B to A的BDe分数 score(set.arc(pdag, from = "A", to = "B"), learning.test) score(set.arc(pdag, from = "B", to = "A"), learning.test)
> score(set.arc(pdag, from = “A”, to = “B”), learning.test) [1] -24006.73 > score(set.arc(pdag, from = “B”, to = “A”), learning.test) [1] -24006.73
从上面的输出中我们可以看到,两个可能的方向的BDe得分是相等的的,所以无法确定A、B两个节点之间的方向。由于贝叶斯网络的定义方式,网络结构必须是有向无环图(DAG);否则 它们的参数无法估计,因为数据的全局概率分布分解为 局部变量(模型中每个变量一个)并不完全已知。
假设我们现在知道了A、B的拓扑序,即B是A的父节点,那么我们可以手动设置该有向弧:
#手动修改B到A的有向弧 dag = set.arc(pdag, from = "B", to = "A") 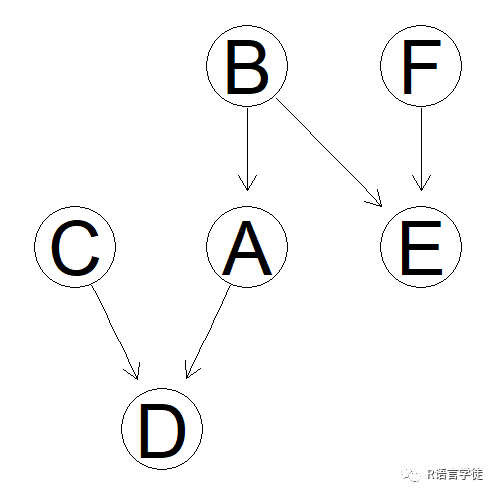
这样,一个完整的贝叶斯网络结构就创建完成了!是不是非常轻松呢,下面小师妹将带大家在建立贝叶斯网络结构的基础上进行参数的拟合和条件概率的推断,贝叶斯网络的参数拟合(或者叫学习)是指在已知节点概率分布族的情况下,通过学习其概率分布族的具体参数给出具体的概率分布,在离散问题中,即指计算出不同节点的条件概率表格(Conditional probability table /CPT),小师妹将使用最大似然估计(mle)的方法向大家演示:
#使用mle进行参数拟合fitted = bn.fit(dag, learning.test, method = "mle")fitted
> fitted
Bayesian network parameters
Parameters of node A (multinomial distribution)
Conditional probability table:
B A a b c a 0.60457240 0.07394366 0.09565217 b 0.31456393 0.64964789 0.26956522 c 0.08086367 0.27640845 0.63478261
Parameters of node B (multinomial distribution)
Conditional probability table: a b c 0.4724 0.1136 0.4140
Parameters of node C (multinomial distribution)
Conditional probability table: a b c 0.7434 0.2048 0.0518
Parameters of node D (multinomial distribution)
Conditional probability table:
, , C = a
A D a b c a 0.80081301 0.09251810 0.10530547 b 0.09024390 0.80209171 0.11173633 c 0.10894309 0.10539019 0.78295820
, , C = b
A D a b c a 0.18079096 0.88304094 0.24695122 b 0.13276836 0.07017544 0.49390244 c 0.68644068 0.04678363 0.25914634
, , C = c
A D a b c a 0.42857143 0.34117647 0.13333333 b 0.20238095 0.38823529 0.44444444 c 0.36904762 0.27058824 0.42222222
Parameters of node E (multinomial distribution)
Conditional probability table:
, , F = a
B E a b c a 0.80524979 0.20588235 0.11937378 b 0.09737511 0.17973856 0.11448141 c 0.09737511 0.61437908 0.76614481
, , F = b
B E a b c a 0.40050804 0.31679389 0.23759542 b 0.49026249 0.36641221 0.50667939 c 0.10922947 0.31679389 0.25572519
Parameters of node F (multinomial distribution)
Conditional probability table: a b 0.5018 0.4982
通过$符号,可以访问指定节点的条件概率分布表,例如通过fitted$D访问节点D的CPT,也可以通过绘图的方式,更为直观地观察我们需要的CPT:
#通过绘图观察CPT bn.fit.barchart(fitted$D) bn.fit.dotplot(fitted$D)
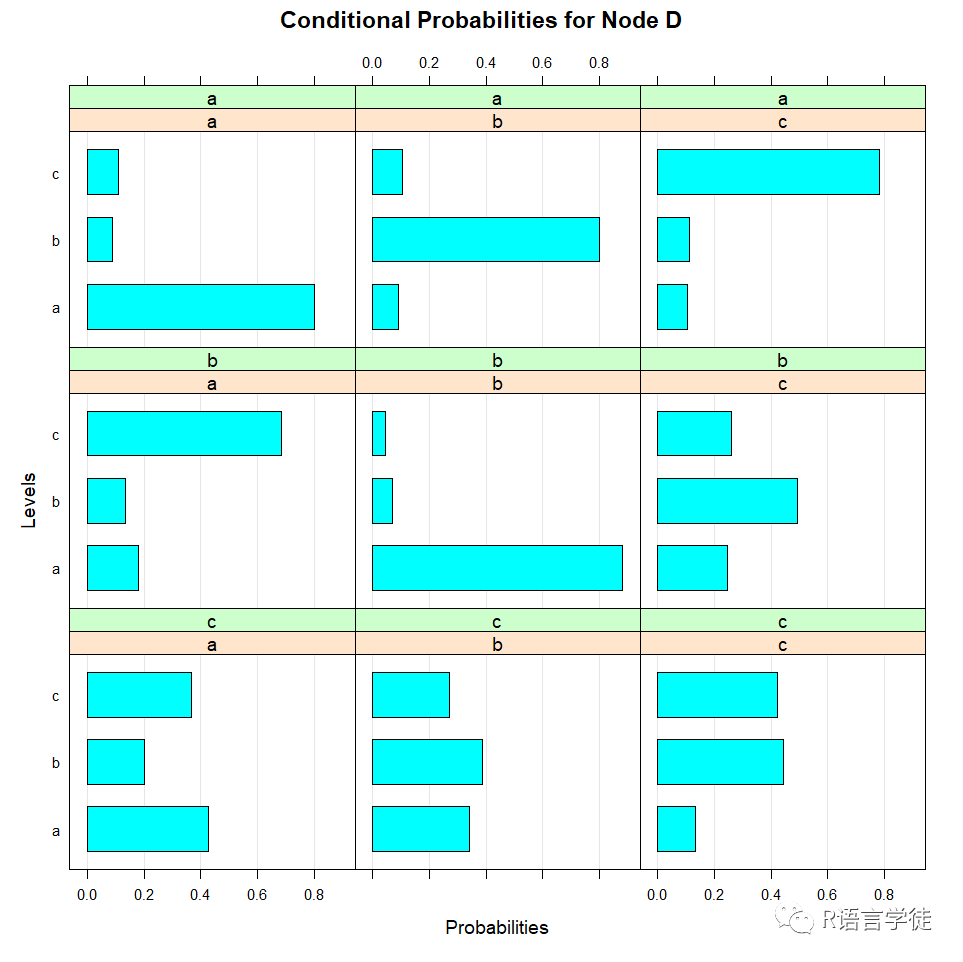
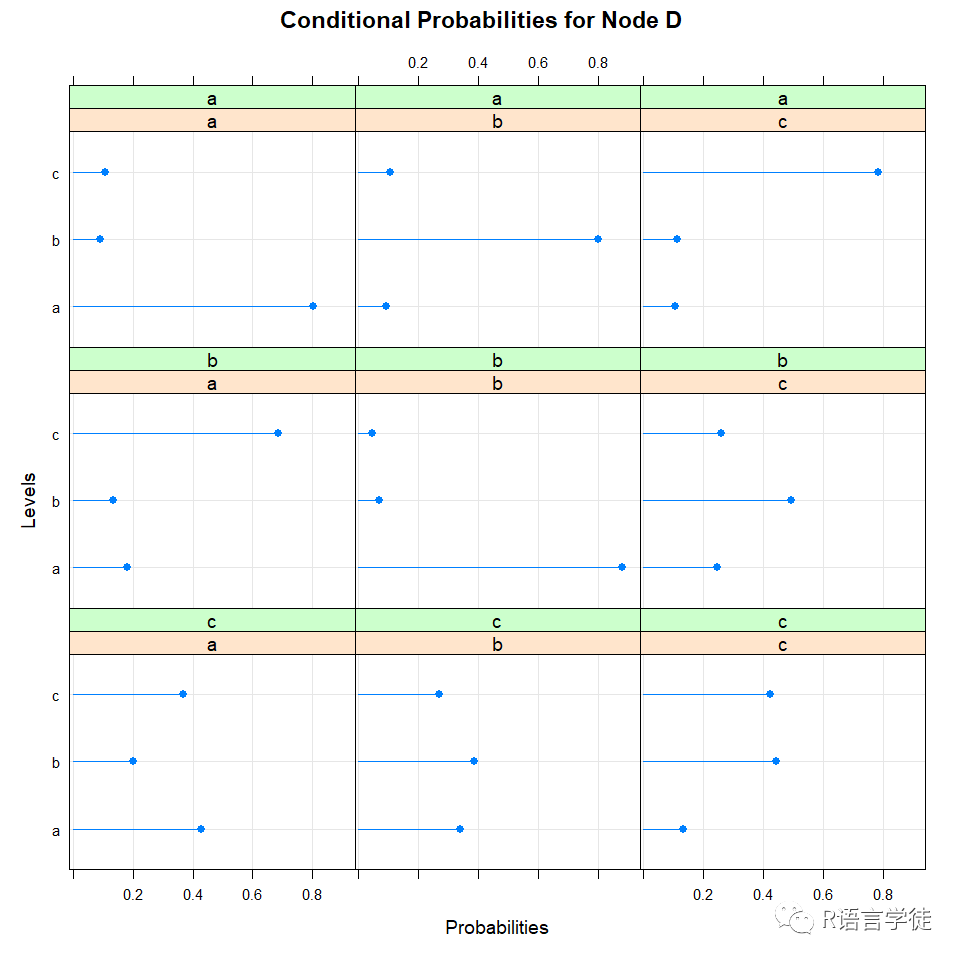
那么,一个简单地通过数据搭建贝叶斯网络结构进而挖掘数据内部的结构关系的例子就完成啦,小伙伴们一定要自己练习一下哦,同时如果大家想要继续了解更多有关R语言内容可以持续关注小师妹哦~~或者也可以关注我们的官网也会持续更新的哦~ http://www.biocloudservice.com/home.html
往期推荐
+
+
+
+