PCA分析是降纬分析中常用的手段,往往大量的数据集不能直观的体现出问题,因此我们需要对数据进行降维处理,分析起到主要作用的指数PCA1、PCA2、PCA3……,因此称为主成分分析。
使用PCA分析的过程中我们需要了解其中的原理,才能更好的理解生物学意义,现在的R包以及一些软件都能做到一键分析的程度,但是我们也要了解背后的原理。本文提供两种做出PCA的方法,一种是理解原理式进行一步步分析,一种为打包好的prcomp()函数、princomp()函数来分析。
一步步做出PCA图
1、数据标准化
为了统一数据的量纲并对数据进行中心化,在主成分分析之间需要对数据进行标准化。
#使用R中自带的鸢尾花作为数据进行实践
data<-iris
head(data)
#用函数scale()进行归一化的处理
dt<-as.matrix(scale(data[,1:4]))
- 计算相关系数矩阵
主成分即找出解释变量方差最大的主成分,所以需要计算变量之间协方差。用cor()进行计算相关系数矩阵
data_cor<-cor(dt)
data_cor
- 特征值特征向量
data_s<-eigen(data_cor)#计算特征值特征向量
data_s
val <- data_s$values #提取主成分部分(即特征向量)values
standard_deviation <- sqrt(val) #换算为sqrt()标准差的形式
pro_v <- val/sum(val)#计算贡献率,作为后边的X和Y轴的标题
- 计算主成分得分
#提取结果中的特征向量
U<-as.matrix(data_s$vectors)
#进行矩阵乘法,获得主成分得分;
pc <-dt %*% U
colnames(pc) <- c(“PC1″,”PC2″,”PC3″,”PC4”)
head(pc)
- 绘制图
#将iris数据集的第5列物种数据加上合并进来;
df<-data.frame(PC,iris$Species)
head(df)
#用ggplot2绘制图
#载入ggplot2包;
library(ggplot2)
#提取主成分的方差贡献率,生成坐标轴标题;
xlab<-paste0(“PC1(“,round(pro_v[1]*100,2),”%)”)#设置x轴的标题
ylab<-paste0(“PC2(“,round(pro_v[2]*100,2),”%)”)#设置y轴的标题
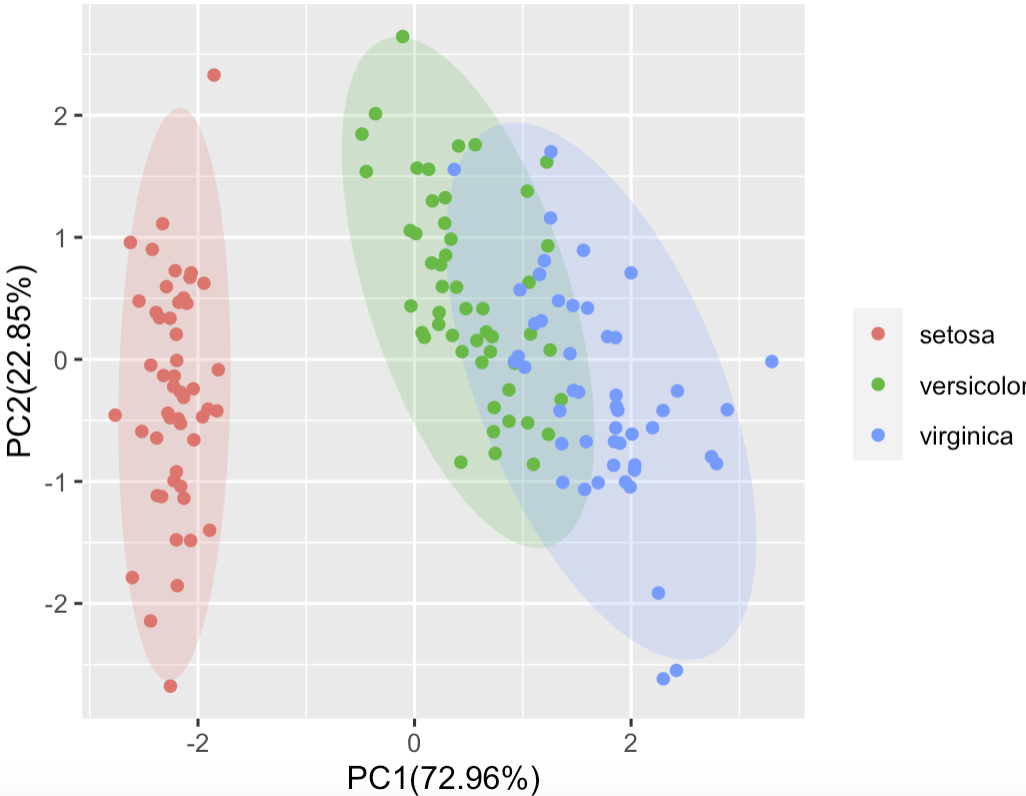
#绘制散点图并添加置信椭圆;
p1<-ggplot(data = df,aes(x=PC1,y=PC2,color=iris.Species))+
stat_ellipse(aes(fill=iris.Species),
type =”norm”, geom =”polygon”,alpha=0.2,color=NA)+
geom_point()+labs(x=xlab,y=ylab,color=””)+
guides(fill=F)
p1
使用现在封装好的函数进行PCA分析
prcomp()函数、princomp()函数可以对上述步骤进行一次性分析
#使用prcomp()函数进行直接PCA的计算
com1 <- prcomp(data[,1:4], center = TRUE,scale. = TRUE)
summary(com1)

后续的需要合并鸢尾花属的列(地5列),最后做出实现PCA可视化即可。
PCA通俗易懂的理解
Principal Component Analysis(PCA)主成分分析它本质是把数据视为一个多维度的存在,但是每个纬度对整个数据集的贡献度是不一样的,为了方便观察,我们会对贡献率低的纬度进行忽略,保留2维或者3维的内容,那留下的三个纬度都是起到重要作用的,因此称为主成分,但是他对于整个数据集的贡献并不是1,所以我们看到横纵坐标并不是1,而是<1的数。
如果我们对于R代码不熟悉的,现在也会有很多网上的小工具一键可以出图http://www.biocloudservice.com/794/794.php
总而言之,我们是要做出图来支撑我们的论文观点,但是对于一些统计学的知识也应该有一定的了解和掌握,才能更好的分析数据、理解图的含义等。
今天的分享就到这里了,小伙伴们如果有什么问题就和小果讨论吧。