上一次小果给大家仔细分享了序列比对的详细过程并且每一步都做了充分的说明,相必小伙伴们都是收获满满,迫不及待地想学习序列比对的原理了吧!这一次小果就来分享序列比对的原理,干货满满的同时可能会稍微有一点难度,但是想要成为生信大神,小伙伴们就不能不了解详细的原理哦~废话不多说,我们直接开始吧!
序列比对问题模型:
来自不同生物体的序列有不同程度的差异,要把它们排列对齐就需要在序列比对不齐的位置插入“空格”或“间隙”,以使其具有相同的长度。
举个例子,假设有以下两个DNA序列GACGGATTAG和GATCGGAATAG。这两个序列之间一个可能的排列如下:

在这种对齐方式下,第一条序列上有一个碱基T在第二条序列上变成了碱基A;第二条序列中多了一个T,通过在第一条序列中添加一个“空格”,使两条序列重新对齐。
如何评价序列比对结果?换句话讲,如何量化两条被比较序列的相似程度?这里引入一个概念:序列一致性,其数值代表进行序列比对时,所选序列当中,相同位点的碱基完全一致的数量占总碱基数的比例。序列一致性最高100%,此时表示序列完全一致。在上面的例子当中,两条序列的一致性为9/11*100%=81.82%(算上补齐的-每条序列11个碱基,从左往右的第三个和第八个碱基对齐失败,共九个对齐成功)。
序列比对的常见类型:
根据比对范围不同,有两种类型的对齐方式:
1. 全局比对:全局比对是将整个查询序列与参考序列进行比对,目标是找到两个序列之间的最优匹配。全局比对适用于具有相对较高的相似性且较长的序列,例如比对整个基因组或全长 cDNA 序列。常用的全局比对算法包括 Needleman-Wunsch 算法和 Smith-Waterman 算法。全局比对会考虑整个序列的匹配、替代和插入/删除信息,因此能够发现较远的亲缘关系和演化信息,但计算成本较高。
2. 局部比对:局部比对是寻找两个序列中的一个或多个片段的最优匹配。局部比对适用于具有较小的片段或存在插入/删除的情况,例如比对已知蛋白质结构中的小片段或找到基因组中的重复序列。常用的局部比对算法是 Smith-Waterman 算法。局部比对将重点放在最佳匹配片段上,因此可以检测到更小的亲缘关系和演化信息,但计算成本也不低。
一般来说,全局比对适用于较长的序列且相似性较高的比对,能够提供更全面的信息,但计算成本较高。而局部比对适用于较短片段或存在变异的比对,可以更准确地找到最佳匹配,但可能会错过全局的演化信息。相对于全局比对和局部比对,Seed-and-Extend(种子扩展)比对方法可以在一定程度上降低计算成本,它的基本原理是首先通过快速的种子匹配过程找到一组可能的匹配位置,然后在这些位置周围进行扩展以寻找最佳匹配。限于篇幅小果在这里就不展开讲解了,感兴趣的小伙伴们可以自行了解哦~
而根据参与比对序列的数量,也有两种不同的比对方式:
1. 成对比对:成对比对是指将成对的测序读段同时与参考序列进行比对。在基因组测序中,通常会对DNA或RNA样本进行双端测序,生成两个相互对应的测序读段(Paired-End Reads)。成对比对的目的是将这两个测序读段同时对齐到参考序列上,以寻找最佳匹配位置。成对比对能够提供更准确的比对结果,可以帮助解决插入片段、结构变异等问题,并提高了结构注释和变异检测的准确性。
2. 多重比对:多重比对是指将多个序列同时进行比对,以找到它们之间的共同模式和共享特征。多重比对通常用于比较多个相关序列(如蛋白质序列、DNA序列或RNA序列)的相似性和差异性。通过多重比对,可以识别出序列之间的保守区域、变异位点、插入/删除事件等信息,从而推断序列的进化关系或功能特征。常用的多重比对算法包括ClustalW、MAFFT和MUSCLE等。
总之,成对比对主要用于测序数据的比对,对于双端测序数据能够提供更准确的重建和结构注释结果。而多重比对则适用于多个相关序列的比较分析,用于研究序列之间的相似性、变异性和进化关系等。
序列比对核心问题:
序列比对的核心问题是寻找最长公共子序列(LCS,Longest Common Subsequence)
当参与比对的序列足够长的时候,比对情况会变复杂,一条序列可能同时比对上多个不同的区域,如何找到最佳匹配情况?举个例子:如抑癌基因p53, 全长超过25kb,比对情况复杂,如何进行比对评价?

我们可以通过寻找最长公共子串或最长公共子序列的方法来解决上述问题。两条序列的最长公共子序列,就是指这两条序列共有的子序列,且长度最长。
以下述两条序列为例:
GACGGATTAG
GATCGGAATAG
这两条序列的LCS是CGGA。当然,我们很容易找到其他长度较短的子序列,如CGG,TAG,但其中最长的是CGGA。一般情况下,参与比对的序列足够长时,可能会出现多个LCS,但此处LCS唯一,长度为4。
LCS非常有助于计算两个序列的相似程度:LCS越长,序列相似度越高。
计分矩阵:
如何设计算法,快速、精准地完成长序列、多序列等复杂比对计算?
我们将被比对序列之间可能的位点关系进行归纳,可以分为以下3类:
1)匹配(|)
2)替换/错配(*)
3)空位(插入/缺失 -)

现在,我们引入另外一个概念,相似性。
相似性的意义与一致性类似,其数值也是用来衡量序列的相似程度。在对DNA序列进行比对时,我们可以采用以下三种不同的核酸序列替换矩阵(计分矩阵)对序列的相似性进行打分:
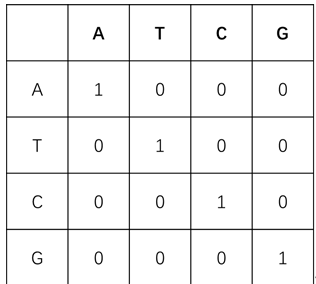
- 等价替换矩阵:相同核苷酸之间的匹配得分为1,不同核苷酸之间的替换得分为0。这种打分方式的优点是简单,但由于没有考虑到实际的统计规律或生物演化规律,实际应用较少
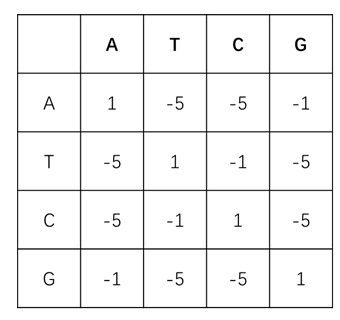
- 转换-颠换矩阵:DNA序列由4种基本的脱氧核糖核苷酸单分子组成,核苷酸分子的核心结构差异是4种含氮碱基,分别是腺嘌呤(Adenine,简称A),鸟嘌呤(Guanine,简称G),胸腺嘧啶(Thymine,简称T),胞嘧啶(Cytosine,简称C)。在数据分析过程中,我们往往用碱基序列指代DNA序列。在生物演化过程中,4种碱基发生相互替换的概率并不均等,嘌呤容易被嘌呤替换(A↔头G),嘧啶容易被嘧啶替换(C↔T),这样的替换被称为转换;嘌呤与嘧啶之间发生替换,则被称为颠换。转换比颠换更容易发生,为体现这样的演化规律,在对序列比对进行打分时,通常对转换赋分为-1,对颠换赋分为-5.
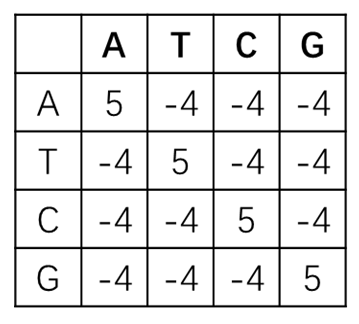
- BLAST矩阵:在实际使用过程中,根据统计经验,将碱基完全相同的情况赋分为5,比对不上的情况赋分为-4,计分矩阵计算所得结果较好,因此将此方法广泛应用于DNA序列比对。
动态规划算法:
我们假设有两个长度分别为m和n的序列S₁和S₂,其中S₁=a₁ a₂ … a(m),S₂=b₁ b₂ … b(n)。
我们将构建一个矩阵A,其中A(i,j)表示a₁ a₂ … a(i)和b₁ b₂ … b(j)的最长共同子序列的长度。
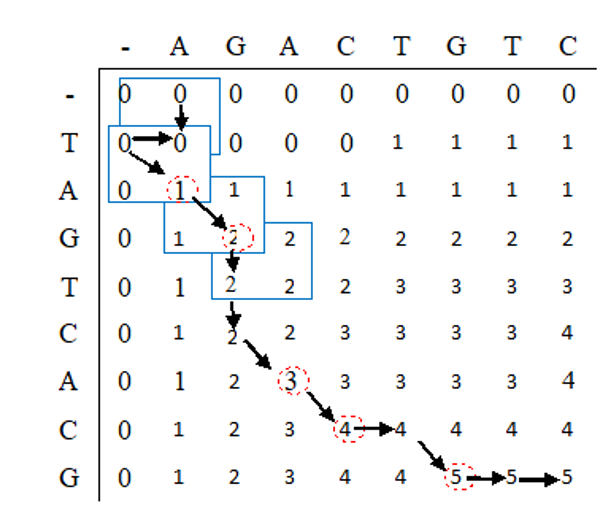
序列S₁是竖着写的,S₂是横着写的。逐行、逐列地将代表行的每个字母与代表列的每个字母进行比较。
1. 如果a(i) = b(j),那么我们就找到了一个匹配(match)。我们为当前的匹配赋值1分;
2. 如果a(i)≠b(j),那么我们就有一个不匹配(mismatch)。
在这种情况下,我们需要考虑两种可能性:由 a₁ … a(i)和b₁ … b(j-1) 得到的LCS,以及由a₁ … a(i-1)和b₁ … b(j)的LCS。
可由以下公式表示:
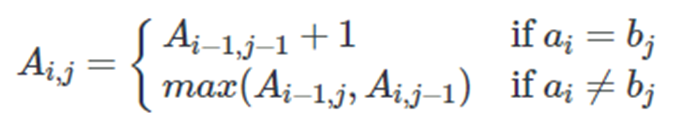
假如小伙伴们还是不太理解动态规划算法,小果在这里举个例子:
“在纸上写下’1+1+1+1+1+1+1+1 =’”
“这个等于多少?”
“是八!”
“在式子左边再写一个’1+’呢?”
“是九!”
“你怎么能这么快知道是九的?”
“因为我只需要让八再加一。”
“所以你不需要从头开始重新数数,因为你记得原来是八!动态规划其实就是一种花哨的说法,它的意思是‘记住现在为以后省时间’。”
看到这里,小果相信小伙伴们已经理解了动态规划算法的核心思想啦,那么动态规划算法如何应用在序列比对中呢?不要着急,我们接着往下看:
Smith-Waterman算法和Needleman-Wunsch算法
动态规划算法在序列比对中最著名的就是Smith-Waterman算法和Needleman-Wunsch算法,这两种算法都是基于动态规划的思想,用于寻找两个序列之间的最佳比对方案。
Smith-Waterman算法可以找到两个序列之间的最佳局部比对方案,即在哪个位置开始,以及从哪个位置结束。以下是算法的具体步骤:
- 构建得分矩阵:根据给定的得分规则(如替换得分、缺失/插入得分等),构建一个大小为(n+1) x (m+1)的得分矩阵,其中n和m分别为两个序列的长度。初始化得分矩阵的所有元素为零。
- 初始化:将得分矩阵的第一行和第一列都初始化为零。同时记录最大得分及其所在的位置。
- 填充得分矩阵:从得分矩阵的第二行和第二列开始,按照以下规则计算每个格子的得分:
- 如果当前比对的两个字符匹配,将左上方格子的得分加上当前字符的得分,作为当前格子的得分。
- 如果当前比对的两个字符不匹配,将左上方格子的得分加上替换得分,作为当前格子的得分。
- 如果当前比对的字符来自缺失序列,将左边格子的得分加上缺失/插入得分,作为当前格子的得分。
- 如果当前比对的字符来自插入序列,将上方格子的得分加上缺失/插入得分,作为当前格子的得分。
- 回溯:从最大得分及其位置开始,按照得分矩阵中的得分规则,回溯找到最佳的比对路径,并生成最佳比对序列。
Needleman-Wunsch算法可以找到两个序列之间的最佳全局比对方案,即从序列的起始位置到结束位置的最佳比对方案。以下是算法的具体步骤:
- 构建得分矩阵:同样根据给定的得分规则,构建一个大小为(n+1) x (m+1)的得分矩阵,其中n和m分别为两个序列的长度。初始化得分矩阵的第一行和第一列,即考虑缺失/插入的情况。
- 填充得分矩阵:从得分矩阵的第二行和第二列开始,按照以下规则计算每个格子的得分:
- 如果当前比对的两个字符匹配,将左上方格子的得分加上当前字符的得分,作为当前格子的得分。
- 如果当前比对的两个字符不匹配,将左上方格子的得分加上替换得分,作为当前格子的得分。
- 如果当前比对的字符来自缺失序列,将左边格子的得分加上缺失/插入得分,作为当前格子的得分。
- 如果当前比对的字符来自插入序列,将上方格子的得分加上缺失/插入得分,作为当前格子的得分。
- 回溯:从得分矩阵的最后一个格子开始,按照得分矩阵中的得分规则,回溯找到最佳的比对路径,并生成最佳比对序列。
看到这里,小伙伴们是不是已经豁然开朗了呢?如果有小伙伴还没有明白,小果建议可以先按照小果上一次分享的内容去试着做一下序列比对的过程,然后再返回来理解原理。当然小伙伴们也可以用小果开发的生信工具平台:http://www.biocloudservice.com/home.html来操作。正如小果一直说的,当大家在新接触一个知识的时候,与其先花费大量时间死啃知识点,不如先利用好工具先自己上手接触流程,在跑完一遍全流程后再返回去理解知识点,相信可以更好更快地理解,达到事半功倍的效果!
今天的分享就到这里啦,下一次小果将给大家介绍如何使用IGV来可视化序列比对的结果,小伙伴们记得关注哦,我们下次再见啦,拜拜┏(^0^)┛~