小伙伴做生存分析的时候避免不了构建Cox回归风险模型,小果告诉大家一个新的方式,小伙伴可以不再用Cox回归了,我们去试试机械学习的方法之一随机森林的生存分析也就是randomForestSRC。我们先了解一下方法,
随机生存森林呢,其实是通过训练大量生存树,以表决的形式,从个体树之中加权选举出最终的预测结果。
构建随机生存森林呢一般有下面几个流程
Ⅰ. 模型通过“自助法”(Bootstrap)将原始数据以有放回的形式随机抽取样本,建立样本子集,并将每个样本中37%的数据作为袋外数据(Out-of-Bag Data)排除在外;
Ⅱ. 对每一个样本随机选择特征构建其对应的生存树;
Ⅲ. 利用Nelson-Aalen法估计随机生存森林模型的总累积风险; Ⅳ. 使用袋外数据计算模型准确度。
下面我们开始吧,我们先按照一下R包,没有的小伙伴先安装一下哦
if (!require(randomForestSRC)) install.packages(“randomForestSRC”)
if (!require(survival)) install.packages(“survival”)
library(randomForestSRC)
library(survival)
我们先读取下示例数据看看,这是R包自带的
下面我们用这几个数据进行学习和展示
data(veteran, package = “randomForestSRC”)
head(veteran)
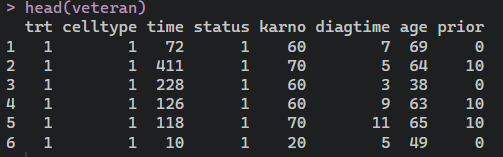
data(pbc, package = “randomForestSRC”)
head(pbc)
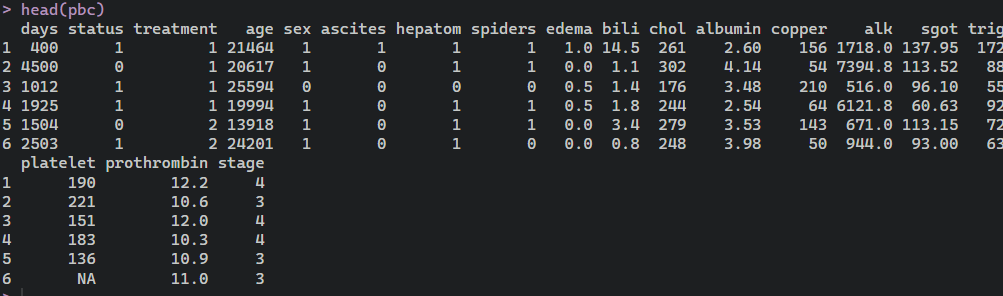
data(wihs, package = “randomForestSRC”)
head(wihs)
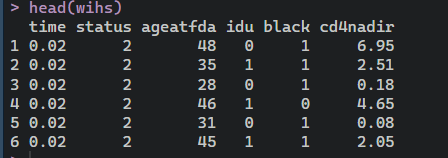
我们使用肺癌的数据集进行分析
肺癌的两种治疗方案的是随机试验
例子一
v.obj <- rfsrc(Surv(time, status) ~ ., data = veteran, ntree = 100, nsplit = 10,
na.action = “na.impute”, tree.err = TRUE, importance = TRUE, block.size = 1)
###设置树的个数为3:
## plot tree number 3
plot(get.tree(v.obj, 3))
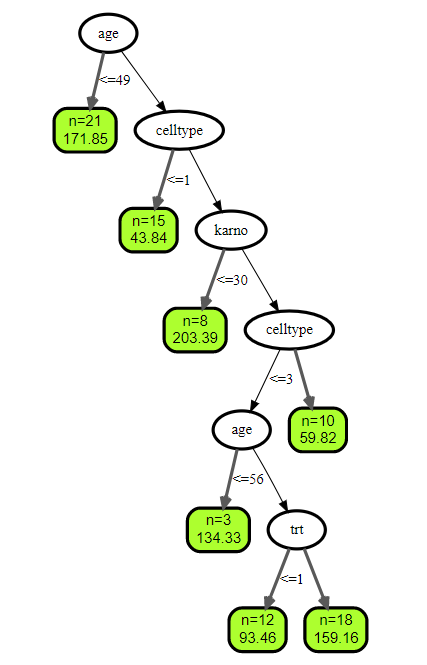
###绘制训练森林的结果
## plot results of trained forest
plot(v.obj)
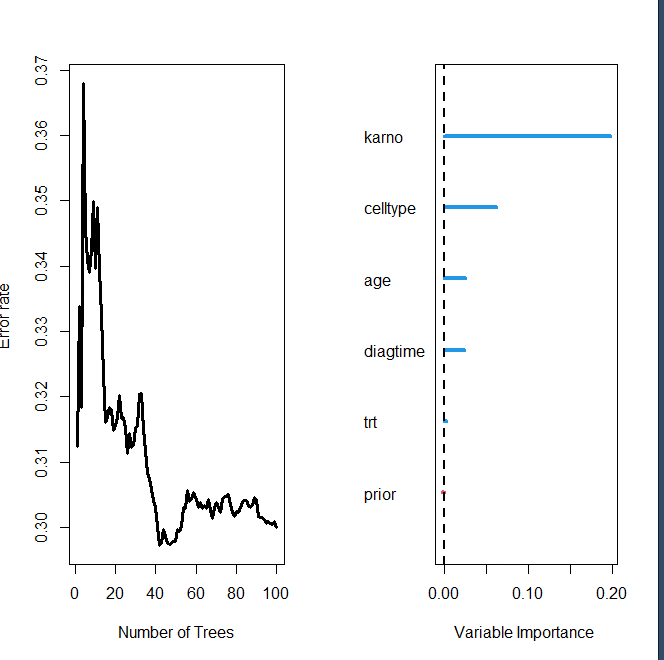
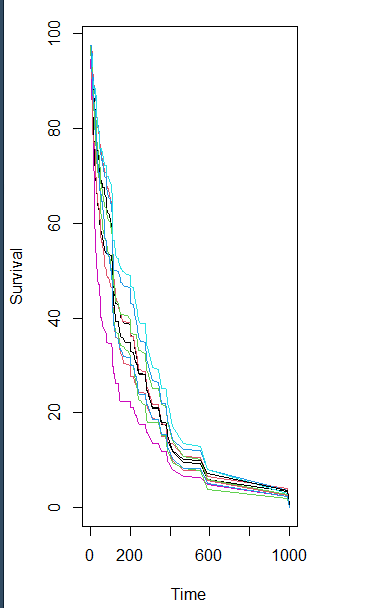
我们直接绘制前10个个体的生存曲线
#绘制前十个个体生存曲线
matplot(v.obj$time.interest, 100 * t(v.obj$survival.oob[1:10, ]), xlab = “Time”,
ylab = “Survival”, type = “l”, lty = 1)
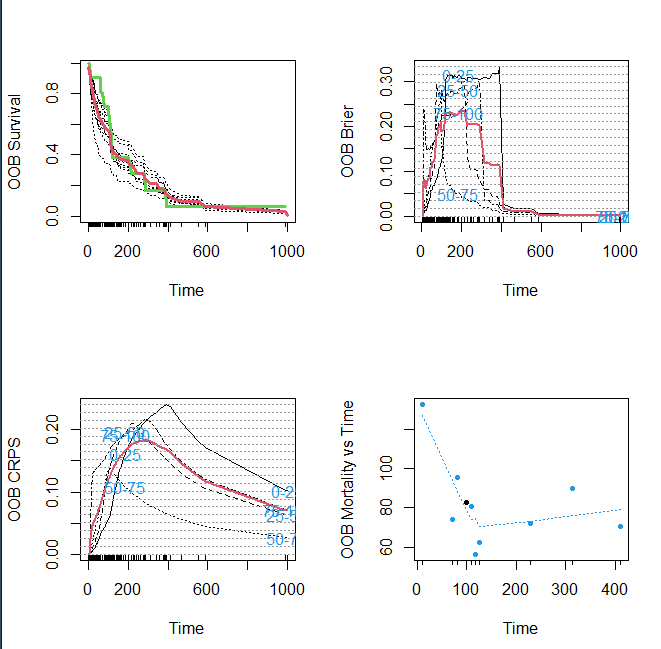
##使用函数plot.survival绘制前10个个体的生存曲线
plot.survival(v.obj, subset = 1:10)
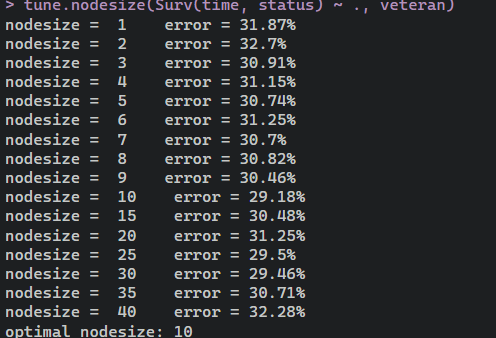
下面我们###快速优化老数据的节点大小##最优的生存节点大小比其他家族#
tune.nodesize(Surv(time, status) ~ ., veteran)
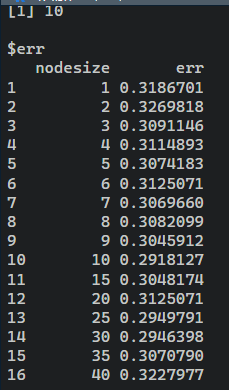
例子2
vd <- veteran
vd$celltype = factor(vd$celltype)
vd$diagtime = factor(vd$diagtime)
vd.obj <- rfsrc(Surv(time, status) ~ ., vd, ntree = 100, nodesize = 5)
plot(get.tree(vd.obj, 3))
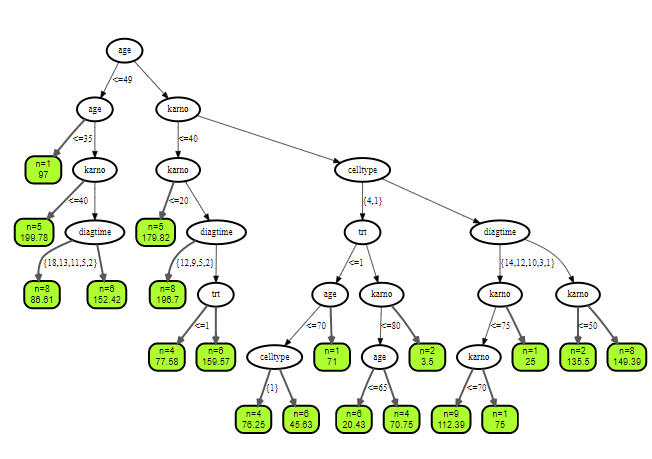
下面我们使用疾病的例子演示
原发性胆汁性肝硬化PBC
来看一下
pbc.obj <- rfsrc(Surv(days, status) ~ ., pbc)
print(pbc.obj)
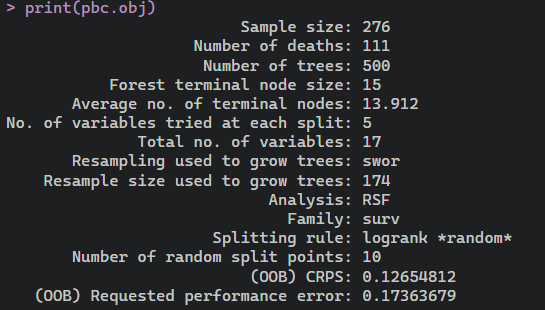
#
pbc.obj2 <- rfsrc(Surv(days, status) ~ ., pbc, nsplit = 10, na.action = “na.impute”)
##与上面相同,但迭代丢失的数据算法
pbc.obj3 <- rfsrc(Surv(days, status) ~ ., pbc, na.action = “na.impute”, nimpute = 3)
## 估算数据的快速方法(不进行推断)
pbc.imp <- impute(Surv(days, status) ~ ., pbc, splitrule = “random”)
我们对两种方法比较一下
比较RF-SRC和Cox回归,说明性能的c指数和Brier评分措施,假设加载了“pec”和“survival”
##比较RF-SRC和COX
require(“survival”)
require(“pec”)
require(“prodlim”)
## pec所需的预测函数
predictSurvProb.rfsrc <- function(object, newdata, times, …) {
ptemp <- predict(object, newdata = newdata, …)$survival
pos <- sindex(jump.times = object$time.interest, eval.times = times)
p <- cbind(1, ptemp)[, pos + 1]
if (NROW(p) != NROW(newdata) || NCOL(p) != length(times))
stop(“Prediction failed”)
p
}
## 数据,公式规范
data(pbc, package = “randomForestSRC”)
pbc.na <- na.omit(pbc) ##remove NA’s
surv.f <- as.formula(Surv(days, status) ~ .)
pec.f <- as.formula(Hist(days, status) ~ 1)
## 运行cox/rfsrc模型进行说明我们使用了少量的树
cox.obj <- coxph(surv.f, data = pbc.na, x = TRUE)
rfsrc.obj <- rfsrc(surv.f, pbc.na, ntree = 150)
## 计算期望Brier分数的bootstrap交叉验证估计
set.seed(17743)
prederror.pbc <- pec(list(cox.obj, rfsrc.obj), data = pbc.na, formula = pec.f, splitMethod = “bootcv”,
B = 50)
print(prederror.pbc)
##
plot(prederror.pbc)
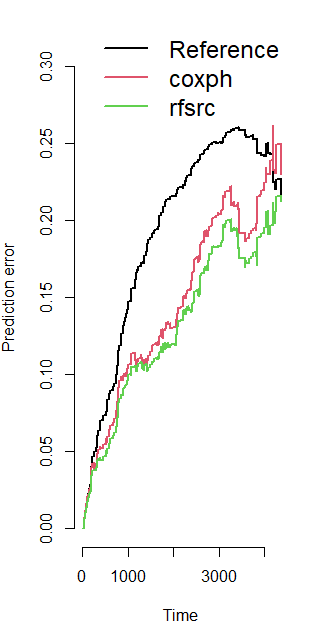
下面我们计算Cox回归
#Cox
## 计算cox回归的袋外C指数并与rfsrc进行比较
rfsrc.obj <- rfsrc(surv.f, pbc.na)
cat(“out-of-bag Cox Analysis …”, “\n”)
## out-of-bag Cox Analysis …
cox.err <- sapply(1:100, function(b) {
if (b%%10 == 0)
cat(“cox bootstrap:”, b, “\n”)
train <- sample(1:nrow(pbc.na), nrow(pbc.na), replace = TRUE)
cox.obj <- tryCatch({
coxph(surv.f, pbc.na[train, ])
}, error = function(ex) {
NULL
})
if (!is.null(cox.obj)) {
get.cindex(pbc.na$days[-train], pbc.na$status[-train], predict(cox.obj, pbc.na[-train,
]))
} else NA
})
cat(“E:\\SXG”)
##
## OOB error rates
cat(“\tRSF : “, rfsrc.obj$err.rate[rfsrc.obj$ntree], “\n”)
## RSF : 0.1714494
cat(“\tCox regression : “, mean(cox.err, na.rm = TRUE), “\n”)
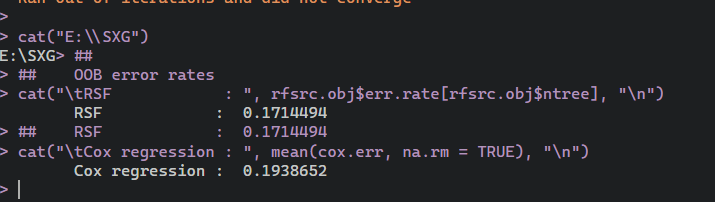
下面我们对生存竞争风险比例模型进行构建
来看一下
#生存竞争风险比例
wihs.obj <- rfsrc(Surv(time, status) ~ ., wihs, nsplit = 3, ntree = 100)
plot.competing.risk(wihs.obj)
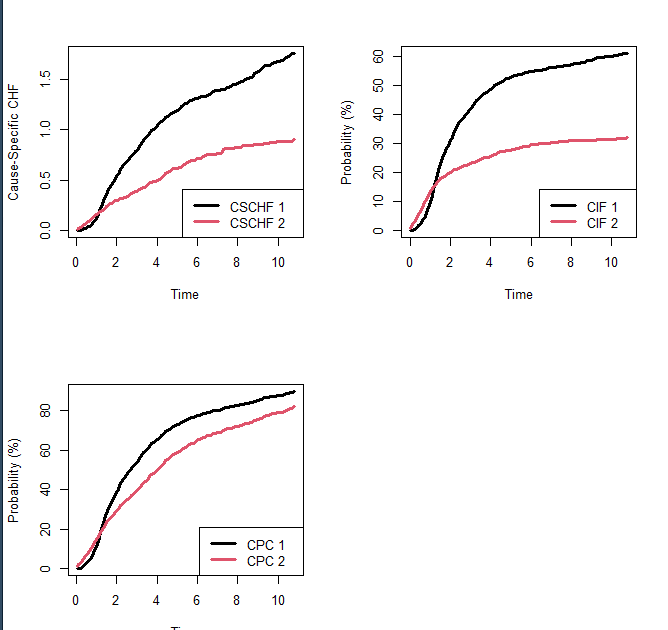
cif <- wihs.obj$cif.oob
Time <- wihs.obj$time.interest
idu <- wihs$idu
cif.haart <- cbind(apply(cif[, , 1][idu == 0, ], 2, mean), apply(cif[, , 1][idu ==
1, ], 2, mean))
cif.aids <- cbind(apply(cif[, , 2][idu == 0, ], 2, mean), apply(cif[, , 2][idu ==
1, ], 2, mean))
matplot(Time, cbind(cif.haart, cif.aids), type = “l”, lty = c(1, 2, 1, 2), col = c(4,
4, 2, 2), lwd = 3, ylab = “Cumulative Incidence”)
legend(“bottomright”, legend = c(“HAART (Non-IDU)”, “HAART (IDU)”, “AIDS (Non-IDU)”,
“AIDS (IDU)”), lty = c(1, 2, 1, 2), col = c(4, 4, 2, 2), lwd = 3, cex = 0.6)#图注
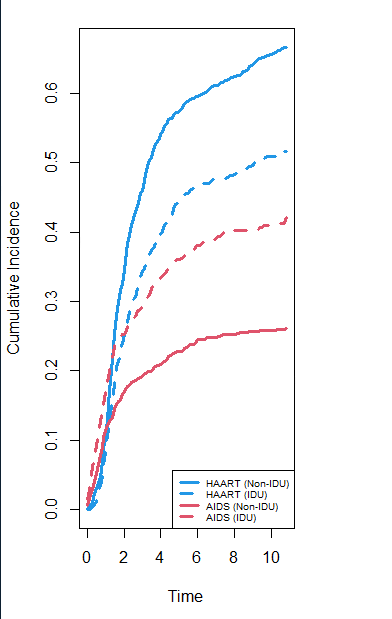
小伙伴可能不太懂结果的含义,小果这里简单解读一些
随机生存森林可以对变量重要性进行排名,VIMP法和最小深度法是最常用的方法:变量VIMP值小于0说明该变量降低了预测的准确性,而当VIMP值大于0则说明该变量提高了预测的准确性;最小深度法通过计算运行到最终节点时的最小深度来给出各变量对于结局事件的重要性。
上述为综合两种方法的散点图,其中,蓝色点代表VIMP值大于0,红色则代表VIMP值小于0;在红色对角虚线上的点代表两种方法对该变量的排名相同,高于对角虚线的点代表其VIMP排名更高,低于对角虚线的点则代表其最小深度排名更高。相较于Cox比例风险回归模型等传统生存分析方法,随机生存森林模型的预测准确度至少等同或优于传统生存分析方法。
随机森林呢其实有很多的优势,小果这里就不一一介绍了,小伙伴学会了吗,将自己的数据去做个实验,动手试试这个新方法吧!
小伙伴多多理解代码的意义哦~