MultiBaC：去除多组学数据批次效应

在生物信息学领域，随研究者开始关注多组学实验。然而，多组学数据中往往存在批次效应，这会导致技术噪声掩盖生物学信号，从而影响数据分析。尽管已有针对单个组学技术的批量效应去除方法，但多组学数据集可能涉及不同批次的数据，这使得组学类型和批次难以区分。此外，在数据采集过程中可能存在系统偏差，导致隐藏的批次效应。因此，我们需要一种能够应对这些挑战的方法。

小果将介绍一款2022年4月28日发表于bioinformatics上名为MultiBaC的R包，它是用于多组学和隐藏批次效应场景中的批量效应去除工具。该包提供多种图形输出，用于模型验证和批量效应校正评估。通过使用MultiBaC R包，研究人员可以更有效地处理多组学实验中的批量效应问题，从而提高数据分析的准确性和可靠性。

MultiBaC：去除多组学数据批次效应
简介
单个组学数据批次效应的修正
关于ARSyN
ARSyN方法概述
示例：酵母表达数据
ARSyNbac输入数据
ARSyNbac校正
ARSyNbac批量效应校正
ARSyNbac去噪
ARSyNbac两种模式
多组学数据集上的批次效应校正
关于MultiBaC
MultiBaC 方法概述
示例：酵母多组学数据集
MultiBaC输入数据
MultiBaC correction
逐步运行MultiBaC步骤
PLS模型拟合
缺失Omics的预测
批次效应校正
ARSyN和MultiBaC结果的可视化
PLS模型中的内部相关性
批次效应估计图
PCA图
总结
参考文献

简介

同时对同一分子系统进行多组学测量（例如转录组学、代谢组学、蛋白质组学或表观基因组学），在一项特定研究中并不总是可能。因此，研究人员有时会结合不同实验室或不同批次产生的兼容数据。在这种情况下，数据通常会受到与实验事件（实验室、批次、技术等）相关的不必要影响，尤其是在高通量分子测定的情况下，这可能会导致噪音严重污染生物信号。这种不必要的变异源通常被称为“批次效应”，并且经常是组学数据集中的第一个变异源，与研究实验条件相比更为突出。
那么，为了从统计分析中获得有意义的结果，消除批次效应就是必要的。如果组学实验设计得当，批次效应与感兴趣的效应（处理、疾病、细胞类型等）不相混淆，所谓的批次效应修正算法（BECAs）可以用来消除或至少减轻系统偏差。因此，这些方法对于整合来自不同实验室的数据或在不同时间测量的数据非常有用。这些BECAs之一是ARSyN方法 [1]，它依赖于ANOVA-Simultaneous Components Analysis (ASCA)框架将组学信号分解为实验效应和其他不需要的效应。ARSyN应用主成分分析（PCA）来估计由批次效应引起的系统变化，然后从原始数据中将其去除。
BECAs传统上应用于消除相同类型组学数据中的批次效应，例如基因表达。然而，用适当的实验设计从单一类型的组学数据中消除批次效应相对简单，但在处理多组学数据集时可能变得不可行。在多组学情况下，每个组学模态可能由不同的实验室或在不同的时间点测量，因此是在不同的批次中获得的。在这种情况下，批次效应会与“组学类型效应”混淆，无法从数据中移除。然而，在某些情况下，多组学批次效应可以得到纠正。MultiBaC是第一个处理多组学数据集中批次效应纠正的BECA。MultiBaC可以消除不同组学s的批次效应，前提是至少有一种常见的组学数据类型包含在所有批次中。
MultiBaC包包含两个BECAs：用于从单个组学数据类型中校正批次效应的ARSyN方法和处理多组学测定批次效应问题的MultiBac方法。

单个组学数据批次效应的修正

关于ARSyN

ARSyN方法概述

ARSyN（ASCA系统性噪声去除）是一种结合了方差分析（ANOVA）和主成分分析（PCA）的方法，用于从估计的ANOVA模型中鉴定出结构变异，这些模型针对的是实验和不需要的效果对 组学数据矩阵的影响。ARSyN可以去除不需要的信号，从而获得经过噪声过滤的数据，以便进行进一步的分析（1）。在MultiBaC包中，ARSyN被用于过滤与已识别或未识别的批次效应相关的噪声。这种适应性被称为ARSyNbac。
在ARSyN方法中，ANOVA模型将每个因素在实验设计中识别的信号与残差分开。该算法可应用于多因素实验设计。如果已知每个样本所属的批次信息，则模型中的一个因素可以是批次。在这种情况下，ANOVA模型将用于将批次效应与其他效应和残差分开。因此，PCA分析将检测到由于批次效应而可能存在的结构化变异，即由解释数据总变异中给定比例的主成分识别的变异，用户可以设置该比例。
此外，当未知批次因子时，也可以应用ARSyN，因为对残差矩阵进行PCA可以检测到与实验设计中未包括的变异源相关的关联结构。当PCA的第一特征值明显高于其他特征值时，我们会注意到残差中的这种信号，因为如果没有任何结构，特征值大致相等。在这种情况下，组件的选择由β参数控制。表示系统性噪声并从原始数据中删除的组件是那些代表平均变异性超过β倍的组件。

示例：酵母表达数据

酵母表达例数据集从Gene Expression Omnibus（GEO）数据库和三个不同的实验室（批次）中收集。在所有这些数据集中，分析了酵母中葡萄糖饥饿的影响。Lab A是Universitat de Valencia的生物化学和分子生物学部门（存取号GSE11521）[2]; Lab B是哈佛大学的分子和细胞生物学部门（存取号GSE56622）[5]; 和Lab C是约翰霍普金斯大学的生物学部门（存取号GSE43747）[6]。
对于每个病例进行适当的数据预处理后，必要时应用了voom转换（使用limma R包）。最后，对来自所有实验室的所有样本进行了TMM归一化。通过从每个数据矩阵中选择200个组学变量并仅从A实验室选择3个样本，获得了减少的数据集。这个酵母多组学减少的数据集包含在MutiBaC包中，用于说明该包的用法。可以使用data(“multiyeast”）指令加载基因表达矩阵。
这三项研究使用了相当的酵母菌株和实验条件，但如图1所示，对表达的主要影响是由于属于不同实验室的数据，即本例中的批次。

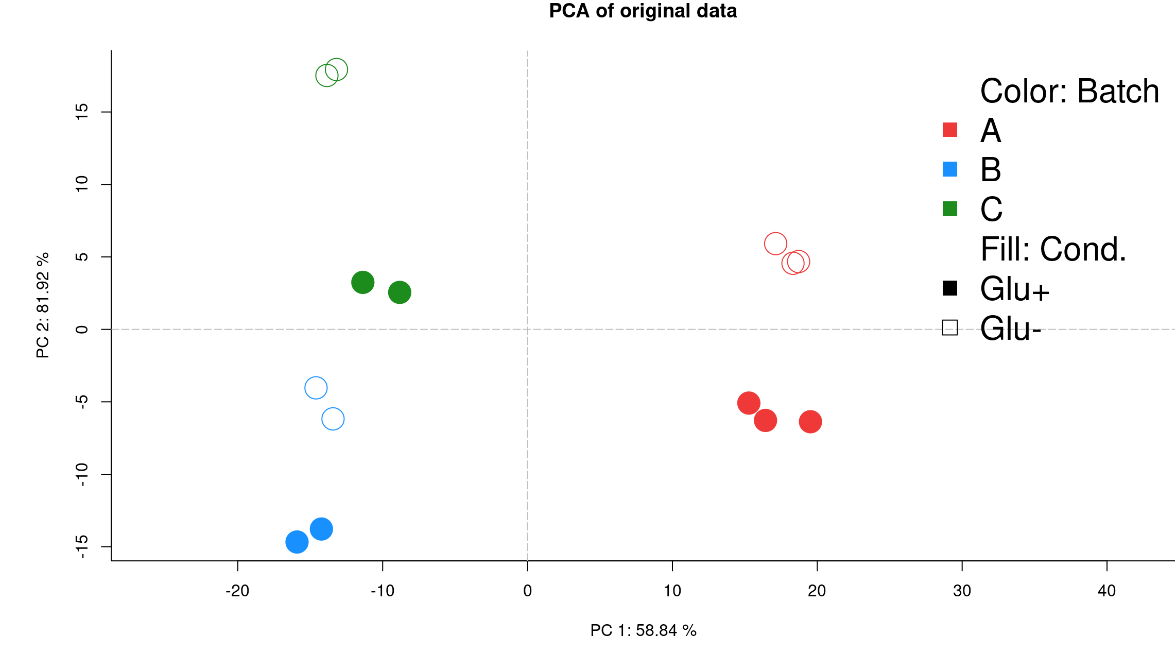
图1：原始基因表达数据的主成分分析图（校正前）批次之间完全分开。使用MultiBaC包生成的图（见结果可视化部分)。

ARSyNbac输入数据

MultiBaC包使用的是MultiAssayExperiment对象，这是Bioconductor为多组学研究提供的一种容器类型，可以从一个由矩阵或data.frame对象组成的列表中创建出来。这些矩阵必须具有以行为特征、以列为样品的布局，如下面所示的酵母示例数据矩阵之一(A.rna)。重要的是，所有数据矩阵都应具有相同的变量空间。如果各组学的变量数量和顺序不一致，那么createMbac函数将会选择共有的变量。因此，所有行必须使用同类型的标识符进行命名。

data(“multiyeast”)
head(A.rna)
## A.rna_Glu+_1 A.rna_Glu+_2 A.rna_Glu+_3 A.rna_Glu-_1 A.rna_Glu-_2
## YOR324C 7.174264 6.976815 7.482661 8.020596 7.736636
## YGL104C 4.239493 4.284775 3.100898 4.957403 3.673252
## YOR142W 8.819824 8.496966 9.026971 10.374525 10.294006
## YOR052C 6.721211 7.011932 7.557519 8.504503 8.586738
## YGR038W 5.878483 5.894121 6.468361 7.856822 7.806318
## YER087W 5.131089 5.295029 5.750657 2.920250 5.496136
## A.rna_Glu-_3
## YOR324C 7.922425
## YGL104C 1.587184
## YOR142W 10.979224
## YOR052C 8.221168
## YGR038W 8.108436
## YER087W 2.879254

对于每个批次（本例中的实验室），需要创建一个“MultiAssayExperiment”对象。新的数据结构“mbac”是一个“MultiAssayExperiment”对象的列表，可以使用包中的“createMbac”函数轻松生成。生成的“mbac”对象将是“ARSyNbac”的输入。

data_RNA<- createMbac (inputOmics = list(A.rna, B.rna, C.rna),
batchFactor = c(“A”, “B”, “C”),
experimentalDesign = list(“A” = c(“Glu+”, “Glu+”,
“Glu+”, “Glu-“,
“Glu-“, “Glu-“),
“B” = c(“Glu+”, “Glu+”,
“Glu-“, “Glu-“),
“C” = c(“Glu+”, “Glu+”,
“Glu-“, “Glu-“)),
omicNames = “RNA”)

以下是createMbac函数参数的说明：

• inputOmics 包含要分析的所有矩阵或数据框对象的列表。也可以提供 MultiAssayExperiment 对象。
• batchFactor 一个向量或因子，指示每个输入矩阵所属的批次（即研究、实验室、时间点等）。如果为 NULL（默认值），则不考虑批次，只可使用 ARSyNbac 噪声减少模式。
• experimentalDesign 包含与批次数量相同的元素的列表。每个元素可以是因子、字符向量或数据框，表示该批次中每个样本的实验条件。当是具有多列（多因素实验设计）的数据框时，不同列将组合成一个单一列，由 MultiBaC 或 ARSyNbac 使用。在任何情况下，实验设置必须对所有批次相同。此外，此列表中元素的名字必须与 batches 参数中声明的名字相同。如果不相同（或为 NULL），则强制将名称与 batches 参数中的名称相同并按相同顺序排列。
• omicNames 每个输入矩阵的名称向量。要求共有的 omic 在所有批次中具有相同的名称。
• commonOmic 批次之间共有的 omic 的名称。必须是 omicNames 参数中的一个名称。如果为 NULL（默认值），将选择所有批次中共有的 omic 名称作为 commonOmic。
  由createMbac函数生成的mbac R结构是一个S3对象，最初只包含一个槽，即ListOfBatches对象。当运行ARSyNbac或MultiBaC函数时，随着它们被创建，这个mbac结构将包含更多的元素。这些新槽是CorrectedData、PLSmodels、ARSyNmodels或InnerRelation，下面进行描述：
• ListOfBatches: 一个包含多个MultiAssayExperiment对象的列表（每个批次一个对象）。
• CorrectedData: 与ListOfBatches结构相同，但是包含修正后的数据矩阵，而不是原始矩阵。
• PLSmodels: 由MultiBaC方法创建的PLS模型（每个非公共omic数据类型一个模型）。仅适用于MultiBaC方法。
• ARSyNmodels: 由ARSyNbac或MultiBaC函数创建的ARSyN模型。
• InnerRelation: 一个类为data.frame的表，包含每个PLS模型在所有组件间的内部相关性（即X（t）和Y（u）矩阵得分间的相关性），用于模型验证。仅适用于MultiBaC方法。
• commonOmic: 批次间公共omic的名称。
  除了绘图之外，还提供了用于可视化mbac对象的其他方法：摘要，它显示了对象的结构。

summary(data_RNA)
## [1] “Object of class mbac: It contains 3 different bacthes and 1 omic type(s).”

	RNA
A	True
B	True
C	True

ARSyNbac校正

MultiBaC包中用于从单一样本数据矩阵中去除批次效应或不需要的噪声的函数是ARSyNbac函数，它允许以下参数：

ARSyNbac (mbac, batchEstimation = TRUE, filterNoise = TRUE,
Interaction=FALSE, Variability = 0.90, beta = 2,
modelName = “Model 1”,
showplot = TRUE)

• mbac: 通过 createMbac 生成的 mbac 对象。
• batchEstimation: 逻辑值。如果为 TRUE（默认值），则估算批次效应并用于校正数据。当已知批次效应的来源时，请使用 TRUE。
• filterNoise: 逻辑值。如果为 TRUE（默认值），则从残差中移除结构化噪声。当数据中存在未知批次效应来源时，请使用此选项。
• Interaction: 逻辑值。是否建立因素之间的交互模型（默认为 FALSE）。
• Variability: 从 0 到 1 的值。每个模型必须解释的数据变异性的最小百分比。在批次校正模式下使用。默认值为 0.90。
• beta: 数值。表示超过平均变异性的 beta 倍的组件被确定为残差中的系统噪声。在噪声减少模式下使用。默认值为 2。
• modelName: 创建的模型的名称。如果您使用 explaine_var 绘图函数，则会显示此名称。默认值为 “Model 1”。
• showplot: 逻辑值。如果为 TRUE（默认值），则显示 explained_var 绘图。此绘图表示 ARSyN 模型选择的组件数量。
  因此，ARSyNbac函数提供了三种分析类型：当提供批次信息时进行ARSyNbac批次效应校正，当批次信息未知时进行ARSyNbac噪声抑制，当存在已知批次效应源和另一个可能的未知不需要的可变性源时进行两者的组合模式。以下部分说明如何进行每一种分析。

ARSyNbac批量效应校正

当在mbac输入对象的batchFactor参数中指定批次时，可以通过选择batchEstimation = TRUE（仅考虑一个批次效应源，filterNoise = FALSE）来估计并消除其影响。此外，通过设置Interaction=TRUE可以研究实验因素与批次因素之间的相互作用。

par(mfrow = c(1,2))
arsyn_1 <- ARSyNbac(data_RNA, modelName = “RNA”, Variability = 0.95,
batchEstimation = TRUE, filterNoise = FALSE, Interaction = FALSE)
plot(arsyn_1, typeP=”pca.cor”, bty = “L”,
pch = custom_pch, cex = 3, col.per.group = custom_col,
legend.text = c(“Color: Batch”, names(data_RNA$ListOfBatches),
“Fill: Cond.”, unique(colData(data_RNA$ListOfBatches$A)$tfactor)),
args.legend = list(“x” = “topright”,
“pch” = c(NA, 15, 15, 15,
NA, 15, 0),
“col” = c(NA, “brown2”, “dodgerblue”, “forestgreen”,
NA, 1, 1),
“bty” = “n”,
“cex” = 1.2))

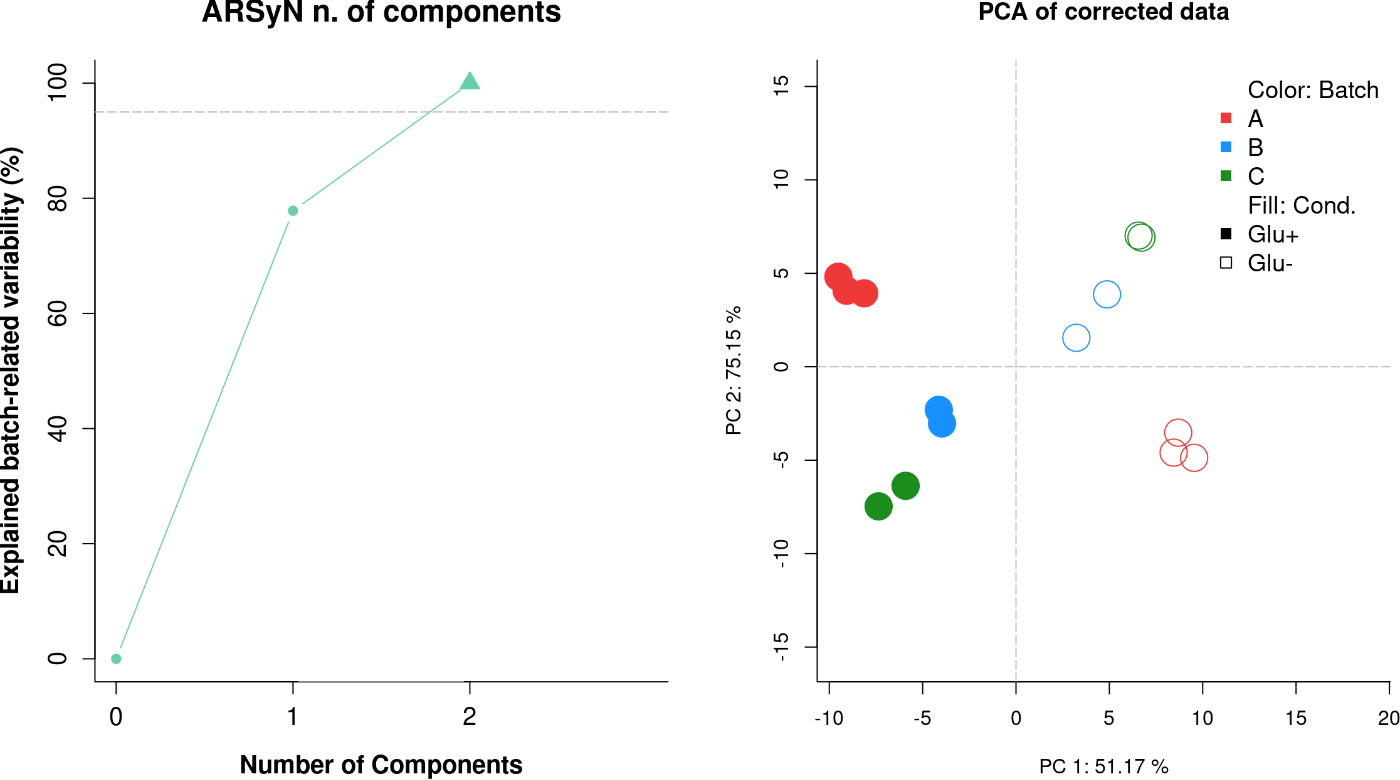
图2：不考虑交互作用批处理时的批次校正
左图：解释方差图。当showplot=TRUE时显示默认图形。该图表示为解释感兴趣效应（批次效应）的某种变异性（y轴）所需的组分数量（x轴）。模型选择的组分数量用三角形符号表示。灰色的虚线表示由Variability参数给出的阈值（百分比）。右图：不考虑批次和条件之间的交互作用时，经过校正的基因表达数据的PCA图。
根据图2的左图，已选择两个主成分（PCs）来解释批次效应总变异的至少95%。右图显示了使用这种分析对修正后的数据进行PCA。现在数据中的主要变异源（PC1)由实验条件决定，而样本不再按批次聚类。

par(mfrow = c(1,2))
arsyn_2 <- ARSyNbac(data_RNA, modelName = “RNA”, Variability = 0.95,
batchEstimation = TRUE, filterNoise = FALSE, Interaction = TRUE)
plot(arsyn_2, typeP=”pca.cor”, bty = “L”,
pch = custom_pch, cex = 3, col.per.group = custom_col,
legend.text = c(“Color: Batch”, names(data_RNA$ListOfBatches),
“Fill: Cond.”, unique(colData(data_RNA$ListOfBatches$A)$tfactor)),
args.legend = list(“x” = “topright”,
“pch” = c(NA, 15, 15, 15,
NA, 15, 0),
“col” = c(NA, “brown2”, “dodgerblue”, “forestgreen”,
NA, 1, 1),
“bty” = “n”,
“cex” = 1.2))

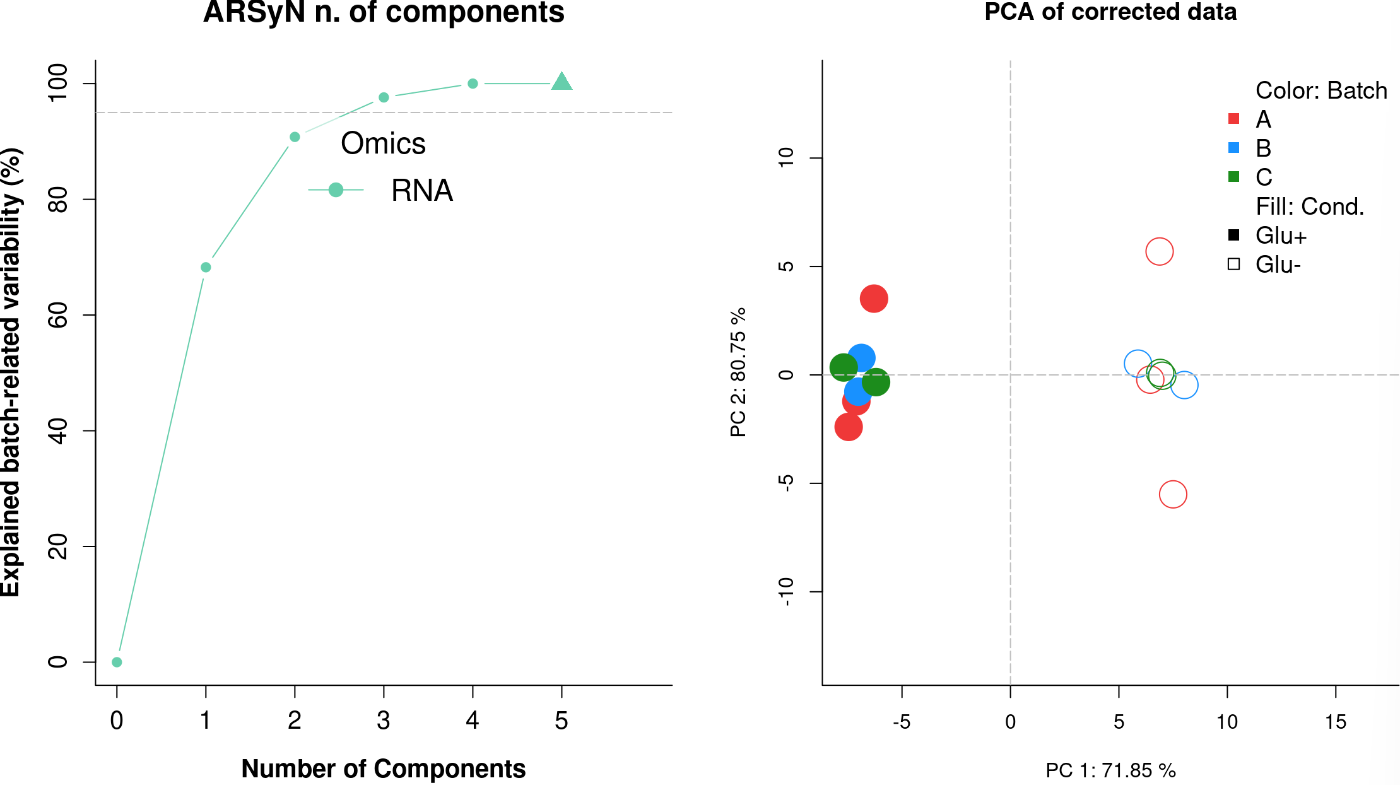
图3：交互作用=TRUE时的批次校正
左图：方差解释图。当showplot=TRUE时，默认显示此图。该图表示为了解释感兴趣的效应（批次效应）的某一部分（y轴）所需的组分数量（x轴）。模型中所选择的组分数量用三角形符号表示。灰色的虚线表示由Variability参数（以百分比形式）给出的阈值。
右图：经过批次条件交互校正后的基因表达PCA图谱。
在图3（右侧面板）中，PC1为负的所有点都对应于Glu-样本，而PC1为正的所有点对应于Glu+样本，正如在模型中不包括相互作用时所发生的情况一样（图2，右侧面板）。然而，在此第二模型中，PC1对数据变异性的解释百分比更高，表明批次效应校正效果更好。一般来说，我们建议使用默认参数（Interaction=FALSE)，因为将部分信号视为批次效应可能导致所需信号的效果被稀释。但是，批次和实验条件之间的相互作用有时可能很强烈，因此我们应该考虑将相互作用包括在模型中，以更好地校正数据。
图1、图2和图3中的PCA图是由MultiBaC包中的自定义plot函数生成的。有关此函数的更多详细信息，请在“ARSyN和MultiBaC结果的视觉呈现”部分查找，其中完整描述了plot函数的所有参数。

ARSyNbac去噪

当batch未被识别时，ARSyNbac通过设置batchEstimation = FALSE和filterNoise = TRUE对残差中系统噪声的存在进行分析。

par(mfrow = c(1,2))
arsyn_3 <- ARSyNbac(data_RNA, modelName = “RNA”, beta = 0.5,
batchEstimation = FALSE, filterNoise = TRUE)
plot(arsyn_3, typeP=”pca.cor”, bty = “L”,
pch = custom_pch, cex = 3, col.per.group = custom_col,
legend.text = c(“Color: Batch”, names(data_RNA$ListOfBatches),
“Fill: Cond.”, unique(colData(data_RNA$ListOfBatches$A)$tfactor)),
args.legend = list(“x” = “topright”,
“pch” = c(NA, 15, 15, 15,
NA, 15, 0),
“col” = c(NA, “brown2”, “dodgerblue”, “forestgreen”,
NA, 1, 1),
“bty” = “n”,
“cex” = 1.2))

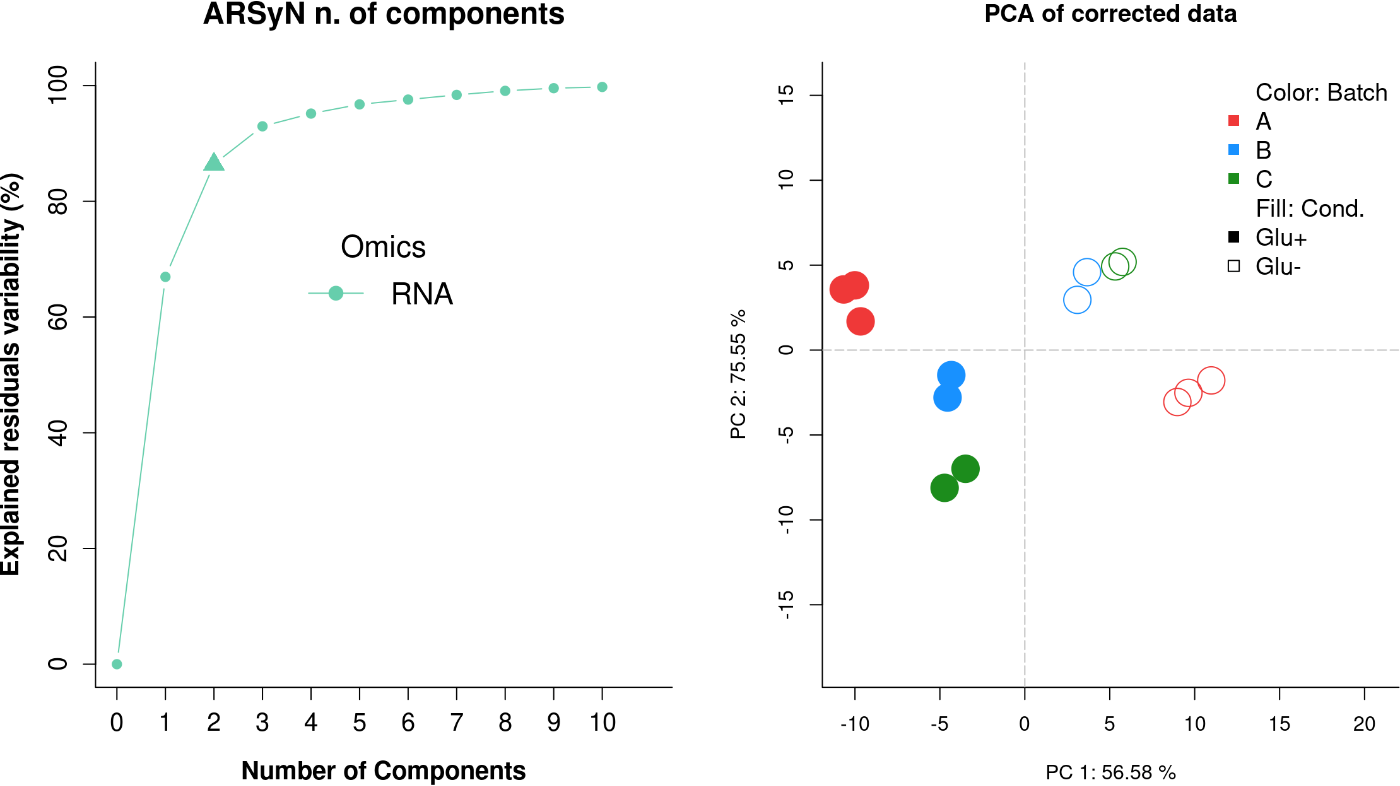
图4：噪声减少模式
左：方差解释图。当 showplot = TRUE 时，默认绘制该图。它表示残差中可变性的百分比（y 轴），由具有给定主成分数目的模型解释（x 轴）。最终模型中选择的组件数用三角形符号表示，并计算为解释 beta 倍残差平均可变性。右：修正基因表达数据的 PCA 图。
在【4】图中，我们可以看到，尽管这个批次被认为是不明确的(batchEstimation=FALSE)，但是ARSyN已经通过估计不需要变化的主要来源，从数据中消除了噪声。在这种噪声减少模式下，我们可以通过beta参数来调整残差中剩余噪声的幅度。基本上，超过beta倍的平均变异性的成分被确定为残差中的系统噪声(在这个模型中选择了3个成分)。因此，beta值越大，导致残差中选择更少的成分。

ARSyNbac两种模式

如果批次效应的来源已知，但可能存在一个额外的未知的不需要的变异源，ARSyNbac可以通过设置batchEstimation = TRUE和filterNoise = TRUE来执行前两种方法。请注意，如果已知的批次效应并不代表我们数据中的主要噪声源，这种模式也可能是有用的。

par(mfrow = c(1,2))
arsyn_4 <- ARSyNbac(data_RNA, modelName = “RNA”, beta = 0.5,
batchEstimation = TRUE, filterNoise = TRUE,
Interaction = TRUE,
Variability = 0.95)
plot(arsyn_4, typeP=”pca.cor”, bty = “L”,
pch = custom_pch, cex = 3, col.per.group = custom_col,
legend.text = c(“Color: Batch”, names(data_RNA$ListOfBatches),
“Fill: Cond.”, unique(colData(data_RNA$ListOfBatches$A)$tfactor)),
args.legend = list(“x” = “topright”,
“pch” = c(NA, 15, 15, 15,
NA, 15, 0),
“col” = c(NA, “brown2”, “dodgerblue”, “forestgreen”,
NA, 1, 1),
“bty” = “n”,
“cex” = 1.2))

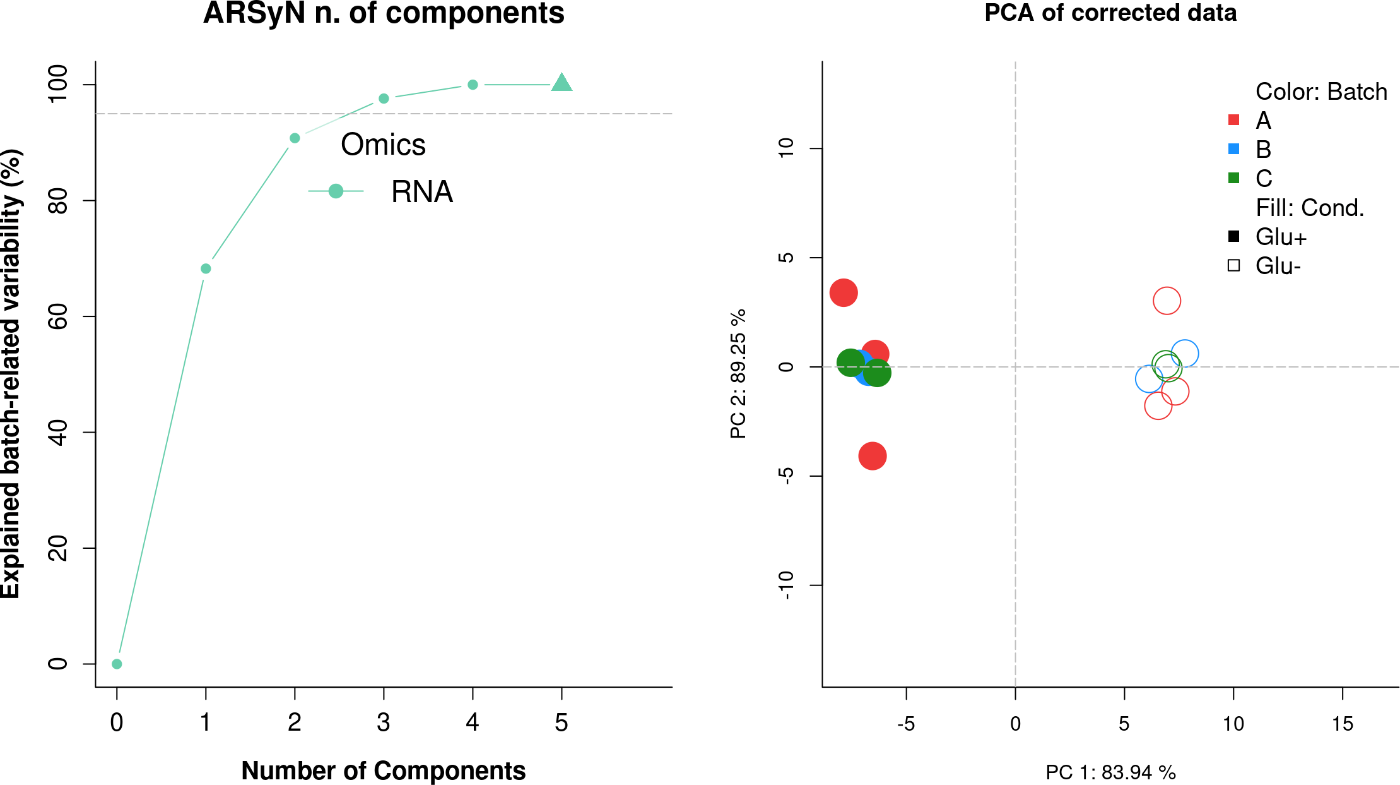
图5：两种模式结合

左图：方差解释图。当 showplot = TRUE 时，默认显示该图。图中表示的是某一模型对残差变异的解释百分比（y轴），随着主成分数目的增加（x轴）。最终模型所选定的主成分数目用三角形符号表示，并计算解释beta倍残差变异的平均值。

右图：修正基因表达数据的PCA图。
在图5中，我们可以看到，同时执行两种方法时，ARSyNbac达到了PC1方差的最大解释率（特别是与图3相比）。在这种模式下，我们可以利用β参数和与解释方差相关的批次效应来调整残差噪声去除的程度。在这个例子中，如图4所示，已知批次效应是主要（几乎是唯一的）不需要的变异源。因此，在其他具有多个批次源的情况下，这种模式的结果可能与之前的两种操作方式非常不同。

多组学数据集上的批次效应校正

关于MultiBaC

MultiBaC 方法概述

MultiBaC是一种从多组学数据中推断细菌群落调控逻辑的计算方法。
多组学数据整合已成为理解生物系统工作机制的流行方法。然而，生成这类数据集仍然成本高且耗时。因此，非常常见的情况是，并非所有样本或组学数据类型同时产生或在同一实验室产生，而是分批进行。此外，当研究团队无法生成自己的多组学数据集时，他们通常从不同的公共存储库收集，因此来自不同的研究或实验室（也是来自不同的批次）。在这两种情况下，都需要事先从这些数据集中去除批次效应以成功进行数据整合。纠正单一数据类型的批次效应的方法无法应用于纠正跨组学的批次效应，因此我们开发了MultiBaC策略，该策略可纠正分布在不同实验室或数据采集事件中的多组学数据集中的批次效应。
然而，对于多组学数据集有一些要求，以便使用MultiBaC去除跨组学的批次效应：

• 每个批次中必须至少有一种常见组学数据类型。例如，我们可能在所有批次中都有基因表达数据测量，然后在每个批次中具有其他不同的组学数据类型。不必要求使用相同的技术来测量共同的组学（例如基因表达）。例如，我们可以有一个批次中的微阵列表达数据和另一个批次中的RNA-seq数据。
• 对于所有常见数据矩阵，组学特征标识符必须相同。例如，我们不能在一个批次中使用Ensembl标识符，而在另一个批次中使用RefSeq。不必要求所有批次中具有相同数量的组学特征，例如基因。MultiBac将从所有常见数据类型矩阵中提取公共标识符以执行分析。
• 在同一批次中，实验设计对于该批次中的所有组学都必须相同，即相同的实验组，具有相同数量的来自相同个体的重复。所有这些样本在所有组学数据矩阵中都必须以相同的顺序排列。

示例：酵母多组学数据集

这些数据包括基因表达数据（RNA），以及由不同实验室分别产生的不同其他组学数据类型。实验室A收集了转录速率数据（GRO，存取号GSE1002）[2]。实验室B获得了翻译速率数据（RIBO，存取号GSE56622）[5]。最后，实验室C测量了全局PAR-CLIP数据（PAR-CLIP，存取号GSE43747）[6]。因此，这些实验室共享一个数据类型（RNA），而其他数据类型则各不相同（GRO、RIBO和PAR-CLIP）。这种分布式多组学方案代表了MultiBaC所解决的校正问题。数据结构的示意图可见于图 6。

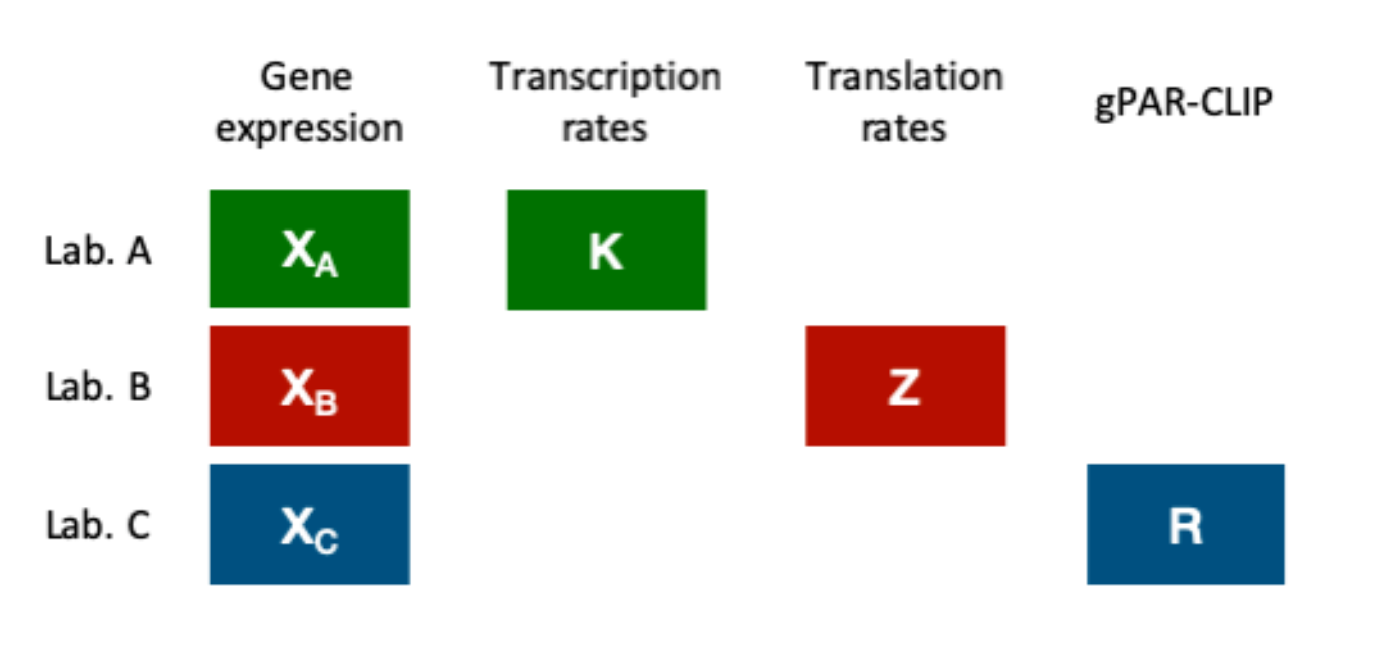
图6：酵母例数据结构的方案
此酵母多组学数据包含在MutiBaC包中，用来说明此包的使用方法。这六个矩阵可以通过使用 data(“multiyeast”)指令来加载。

MultiBaC输入数据

如前所述，MultiBaC包使用MultiAssayExperiment对象，这是Bioconductor中用于多组学研究的一种容器类型，可以从一个由矩阵或data.frame对象组成的列表中创建。这些矩阵必须具有以行为特征、以列为样本的特点（请参见ARSyNbac部分中的示例）。由于MultiBaC在相同批次的不同组学之间计算回归模型，因此重要的是来自相同批次的所有矩阵必须具有相同的实验设计：相同数量的样本并以相同的顺序排列。MultiBaC也涉及不同批次的不同组学的共信息。因此，如果组学变量的数量和顺序不同，则MultiBaC将选择共有的变量用于模型。因此，必须使用相同类型的标识符对行进行命名。
要生成作为MultiBaC函数输入的mbac对象，可以使用包中的createMbac函数，轻松便捷地完成这项任务。

my_mbac <- createMbac (inputOmics = list(A.rna, A.gro,
B.rna, B.ribo,
C.rna, C.par),
batchFactor = c(“A”, “A”,
“B”, “B”,
“C”, “C”),
experimentalDesign = list(“A” = c(“Glu+”, “Glu+”,
“Glu+”, “Glu-“,
“Glu-“, “Glu-“),
“B” = c(“Glu+”, “Glu+”,
“Glu-“, “Glu-“),
“C” = c(“Glu+”, “Glu+”,
“Glu-“, “Glu-“)),
omicNames = c(“RNA”, “GRO”,
“RNA”, “RIBO”,
“RNA”, “PAR”))

有关“createMbac”函数的更多详细信息，请参见ARSyNbac输入数据部分。需要注意的是，我们不需要指明哪个是常见的omic（在commonOmic参数中），因为对于所有批次（实验室）来说，只有一个共同的omic（RNA），并且该函数将其检测为常见的omic。

MultiBaC correction

一旦使用“createMbac”函数创建了mbac对象，就可以将其用作“MultiBaC”函数的输入数据（以mbac参数的形式），而“MultiBaC”函数是用于校正多组学批次效应的包装函数。

MultiBaC (mbac,
test.comp = NULL, scale = FALSE,
center = TRUE, crossval = NULL,
Interaction = FALSE,
Variability = 0.90,
showplot = TRUE,
showinfo = TRUE)

MultiBaC函数的参数对应于MultiBaC方法的各个步骤：

• mbac: 由 createMbac 生成的 mbac 对象。
• test.comp: PLS 模型允许的最大组件数。如果为 NULL（默认），则使用矩阵的最小有效秩作为最大组件数。
• scale: 逻辑值。是否需要对 X 和 Y 矩阵进行缩放。默认值为 FALSE。
• center: 逻辑值。是否需要对 X 和 Y 矩阵进行中心化。默认值为 TRUE。
• crossval: 整数：交叉验证段数。样本数（“x”的行数）必须 >= crossvalI。如果为 NULL（默认），则执行 leave-one-out 交叉验证。
• Interaction: 逻辑值。是否在 ARSyN 模型中建立实验因素和批次因素之间的相互作用模型。默认值为 FALSE。
• Variability: 从 0 到 1 的最小百分比数据变化性，对于每个 ARSyN 模型必须解释。默认值为 0.90。
• showplot: 逻辑值。如果为 TRUE（默认），则显示 Q2 和解释方差图。
• showinfo: 逻辑值。如果为 TRUE（默认），则显示函数进度信息。
  下面显示了使用MultiBaC函数对酵母示例数据进行处理的情况：

my_final_mbac <- MultiBaC (my_mbac,
test.comp = NULL, scale = FALSE,
center = TRUE, crossval = NULL,
Interaction = TRUE,
Variability = 0.9,
showplot = TRUE,
showinfo = TRUE)
## Step 1: Create PLS models
## – Model for batch A
## – Model for batch B
## – Model for batch C
## Step 2: Generating missing omics
## Step 3: Batch effect correction using ARSyNbac
## [1] “Table: Inner correlation between scores for each PLS model computed.”
##
##
## A: GRO B: RIBO C: PAR
## ————- ———- ———- ———-
## Component: 1 0.9471967 0.9987790 0.9396986
## Component: 2 0.9277123 0.9991239 0.9998556
## Component: 3 0.9992129 1.0000000 1.0000000
## Component: 4 0.9999867 NA NA
## Component: 5 1.0000000 NA NA

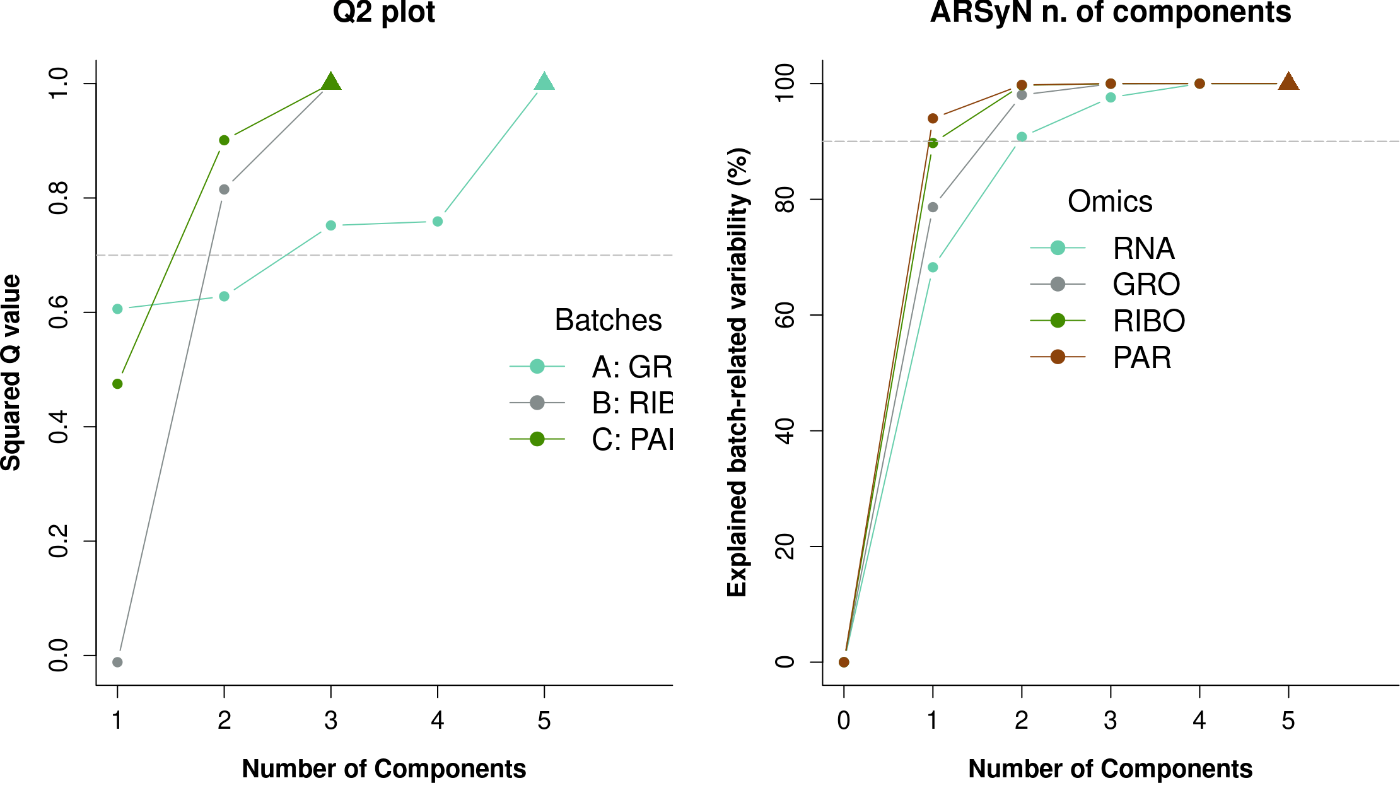
图7：Q2和方差解释图

Q2图（左）显示了达到一定Q2值所需的组件数量（x）（y）。每个模型所选的组件数量用三角形符号表示。灰色的虚线表示0.7的Q2阈值。方差解释图（右）表示了要解释感兴趣的效应（批次效应）的某个变异性（y）所需的组件数量（x）。每个模型所选的组件数量用三角形符号表示。灰色的虚线表示方差参数的百分比。
默认情况下（showinfo = TRUE），会显示包含PLS模型内部相关性的表格。此外，默认的图形（showplot = TRUE）是“Q2图”和“方差解释图”（参见图7），其中包含有关MultiBaC性能的重要信息。“Q2图”表示PLS模型预测能力的Q2²分数。x轴表示提取的PLS模型的组件数，y轴为Q2²值。MultiBaC方法的性能将随着Q2²值的增加而提高，因为Q2²值高表明PLS对缺失omics的预测良好，因此可以更好地估计批次效应。请注意，根据矩阵的秩，每个PLS模型可能具有不同的最大组件数。“方差解释图”提供了使用ARSyN方法提供的ASCA分解解释的与批次效应相关的变异性。x轴表示提取的ASCA模型的组件数，y轴反映了解释方差的百分比。在这种情况下，较高的解释方差导致更好的批次效应估计。在这两个图中，每个模型所选的组件数用三角形符号表示。在“Q2图”中，所选的组件数是最大化Q2值的组件数，而在“方差解释图”中，这个数字是最小数量达到高于函数Variability参数的解释方差（灰色的虚线）的组件数。

逐步运行MultiBaC步骤

MultiBaC的所有不同步骤都可以使用特定函数从初始的mbac对象独立计算。MultiBaC策略可以分为三个主要步骤，下面将详细描述：1) PLS模型拟合，2) 缺失omics的预测，3)批次效应修正。
以下是您要求的段落的翻译：

PLS模型拟合

genModelList函数在不同和常见的omic数据类型之间生成PLS模型，并通过交叉验证方法计算最佳组件数。

my_mbac_2 <- genModelList (my_mbac, test.comp = NULL,
scale = FALSE, center = TRUE,
crossval = NULL,
showinfo = TRUE)
## – Model for batch A
## – Model for batch B
## – Model for batch C

genModelList函数的参数为：

• mbac: 属于mbac类型对象。
• test.comp: PLS模型中允许的最大组件数。如果为NULL（默认值），则使用矩阵的最小有效秩作为最大组件数。
• scale: 逻辑值。是否需要对X和Y矩阵进行缩放。默认值为FALSE。
• center: 逻辑值。是否需要对X和Y矩阵进行中心化。默认值为TRUE。
• crossval: 指示交叉验证段数的整数。样本数（“x”的行数）必须大于等于crossvalI。如果为NULL（默认值），则进行leave-one-out交叉验证。
• showinfo: 逻辑值，指示是否显示函数进度信息。默认值为TRUE。
  genModelList的输出是一个带有新槽PLSmodels的mbac对象，该槽是使用ropls包获得的PLS模型的列表。输出的每个槽对应于ListOfBatches中的一个批次。如果一个批次包含多个非公共omic，则genModelList中的“批次”元素将依次包含与该批次中的非公共omic数量相等的元素，即每个非公共omic一个PLS模型。

缺失Omics的预测

利用genModelList函数输出中的genMissingOmics函数，对初步缺失的Omics进行预测。

multiBatchDesign <- genMissingOmics(my_mbac_2)

运行genMissingOmics函数后得到的结果是一个MultiAssayExperiment结构列表。在这种情况下，每个批次都包含MultiBaC中引入的所有Omics。例如，如果正在研究两个批次“A”和“B”，其中“A”包含“RNA-seq”和“GRO-seq”数据，而“B”包含“RNA-seq”和“Metabolomics”数据，则在应用genMissingOmics函数后，批次“A”将包含“RNA-seq”，“GRO-seq”以及预测的“Metabolomics”数据。

批次效应校正

my_finalwise_mbac <- batchCorrection(my_mbac_2,
multiBatchDesign = multiBatchDesign,
Interaction = TRUE,
Variability = 0.90)

如前所述，ARSyN对数据矩阵进行类似ANOVA的分解，以估计批次效应，然后在每个子矩阵上应用PCA。每个PCA的主成分数量通过“Variability”参数进行调整。该函数的输出由两个不同的对象组成：CorrectedData和ARSyNmodels。前者与“ListOfBatches”槽的结构相同。然而，在这种情况下，所有批次都包含MultiBaC中引入的所有 omics，这是通过对每个omics数据类型分别进行批次效应校正后得到的。请注意，我们丢弃了预测的omics矩阵，只在后续的统计分析中使用经过校正的原始矩阵。ARSyNmodels槽包含每个omics数据类型的ASCA分解模型。

ARSyN和MultiBaC结果的可视化

如前所述，ARSyNbac和MultiBaC的输出是mbac类型的对象。由于mbac类包含绘图方法，因此可以将plot函数应用于mbac对象，以图形方式显示有关方法和数据特征的性能的附加信息。mbac对象的plot*函数接受几个额外的参数：

plot (x, typeP = “def”,
col.by.batch = TRUE,
col.per.group = NULL,
comp2plot = c(1,2),
legend.text = NULL,
args.legend = NULL, …)

描述参数：

• x: 由MultiBaC方法返回的“mbac”类对象。
• typeP: 要显示的图形的类型。选项有：“def” （默认选项，对于MultiBaC是“Q2 plot”和“Explained variance plot”，对于ARSyNbac输出是“Explained variance plot”） 、“inner”（对于MultiBaC输出，是每个PLS模型的内部相关性图）、“pca.org”（对于MultiBaC或ARSyNbac输出，是原始数据的PCA图）、“pca.cor”（对于MultiBaC或ARSyNbac输出，是修正数据的PCA图）、“pca.both”（对于MultiBaC或ARSyNbac输出，是原始和修正数据的PCA图）以及“batch”（对于所有输出，是“Batch effect estimation”图）。请注意，当所有omics共享相同的变量空间时（例如，为所有数据矩阵提供基因标识符作为变量名），才能生成PCA图。
• col.by.batch: PCA图的参数。TRUE或FALSE。如果为TRUE（默认），则样本按批次因素着色。如果为FALSE，则样本按实验条件着色。
• col.per.group: PCA图的参数。每个组的颜色（由批次或实验条件给出）。如果为NULL（默认），则颜色从预定义调色板中选取。
• comp2plot: PCA或InnerRel图的参数。指示要绘制的组件。默认是c(1,2)，这意味着在PCA图中，第1个组件绘制在“x”轴上，第2个组件绘制在“y”轴上，对于InnerRel图，要显示第1和第2个组件的内部关系图。如果指示了多个组件，则函数将返回所需数量的图以显示所有组件。
• legend.text: 用于构造图例的文本向量。PCA图的参数。如果为NULL（默认），则使用包含在mbac对象中的批次或条件名称。
• args.legend: legend()函数的附加参数列表；列表中的名称用作参数名称。仅在legend.text被提供时使用。
• …: 其他图形参数。
  虽然 plot 函数可以生成上述所有类型的图，但每个图也可以通过其对应的函数独立生成，这些函数包括：Q2_plot (mbac)、explained_varPlot (mbac)、plot_pca (mbac, typeP = c(“pca.org”, “pca.cor”, “pca.both”), col.by.batch, col.per.group, comp2plot, legend.text, args.legend)、batchEstPlot (mbac)以及 inner_relPlot (mbac, comp2plot = c(1,2)).
  所有这些图都有助于验证和理解MultiBaC或ARSyNbac的性能。所有这些图都可以使用MultiBaC的输出，而显示与PLS模型相关的信息图则不适用于ARSyNbac的输出（请参见typeP参数）。
  除了“Q2 plot”和“Explained variance plot”（图7）是默认绘制的，并且在前面部分介绍过，后面部分用于描述MultiBaC包中的其他图表。

PLS模型中的内部相关性

在MultiBaC中需要验证的一个重要方面是PLS模型中X和Y分数之间的内在相关性。正如我们之前指出的那样，《MultiBaC》函数默认情况下以数值形式显示此信息，但也可以调用可视化表示。

plot (my_final_mbac, typeP = “inner”, comp2plot = c(1,2))
## Hit <Return> to see next plot:
## Inner correlation of scores. Batch: A; Model for omic: GRO
## Warning in par(initpar): graphical parameter “cin” cannot be set

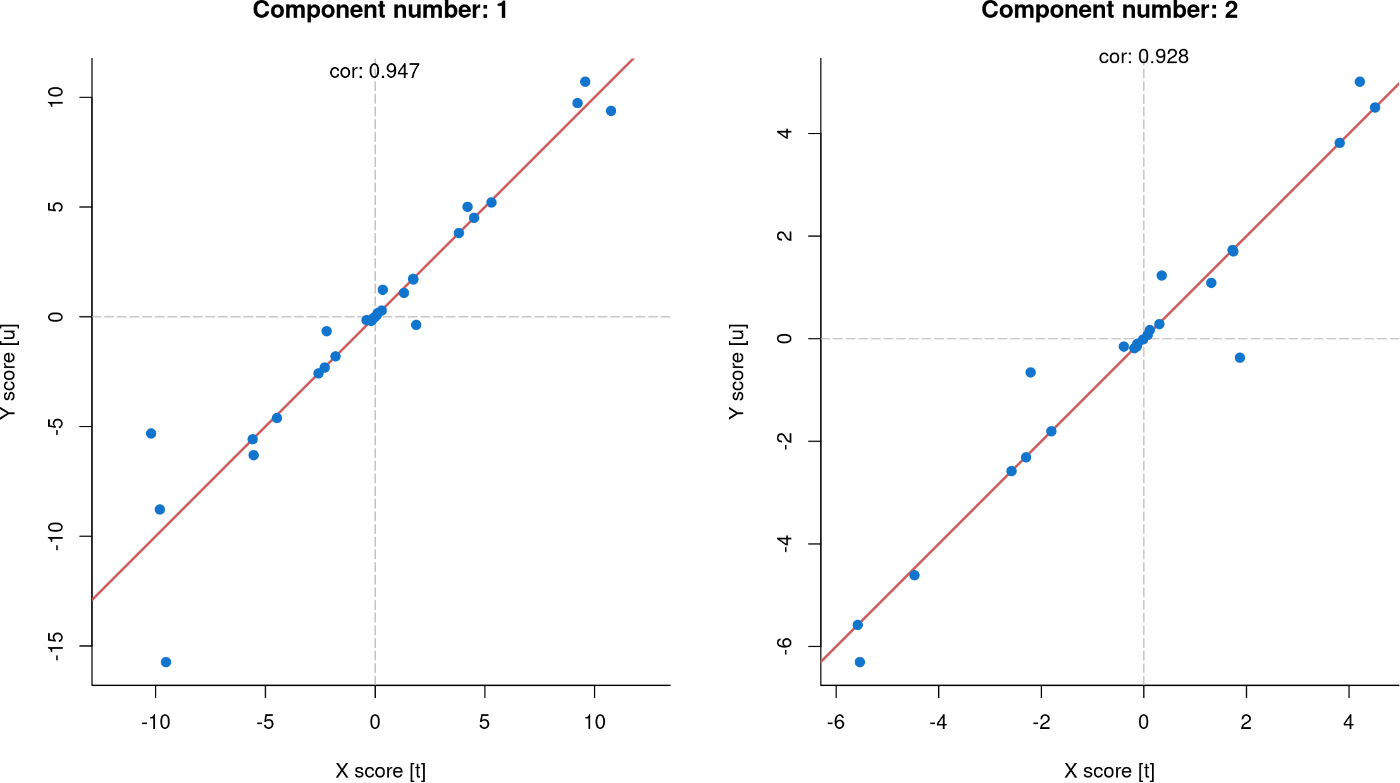
图8：PLS组件内部关系的绘图
仅以批次“A”为例显示结果。每个面板表示PCA模型的一个组件的内部相关性。红线表示对角线，此时相关性最大（1：1）。
如图8所示，PLS模型中与“A”批次中两种组学数据类型均相关的内部相关性得分。虽然我们仅展示了“A”批次的散点图，但通过运行plot（typeP = “inner”）命令，MultiBaC性能中生成的PLS模型的所有内部相关性图都将以“Hit to see next plot:”标签显示，因此需要用户交互才能显示完整的一组图形。模型的相关信息（包括批次和组学）也会在R提示符中显示。“内部相关性图”是一个关键结果，因为它代表了PLS模型的验证。在每个成分中，x分数（t）和y分数（u）之间的相关性应该是线性的，如图8所示。如果观察到非线性相关性，则需要对数据进行转换。

批次效应估计图

此图显示了估计批次效应的幅度。通常，在执行MultiBaC或ARSyNbac之前使用此图，因为它只需要createMbac函数返回的mbac基本数据。

plot (my_final_mbac, typeP = “batch”)

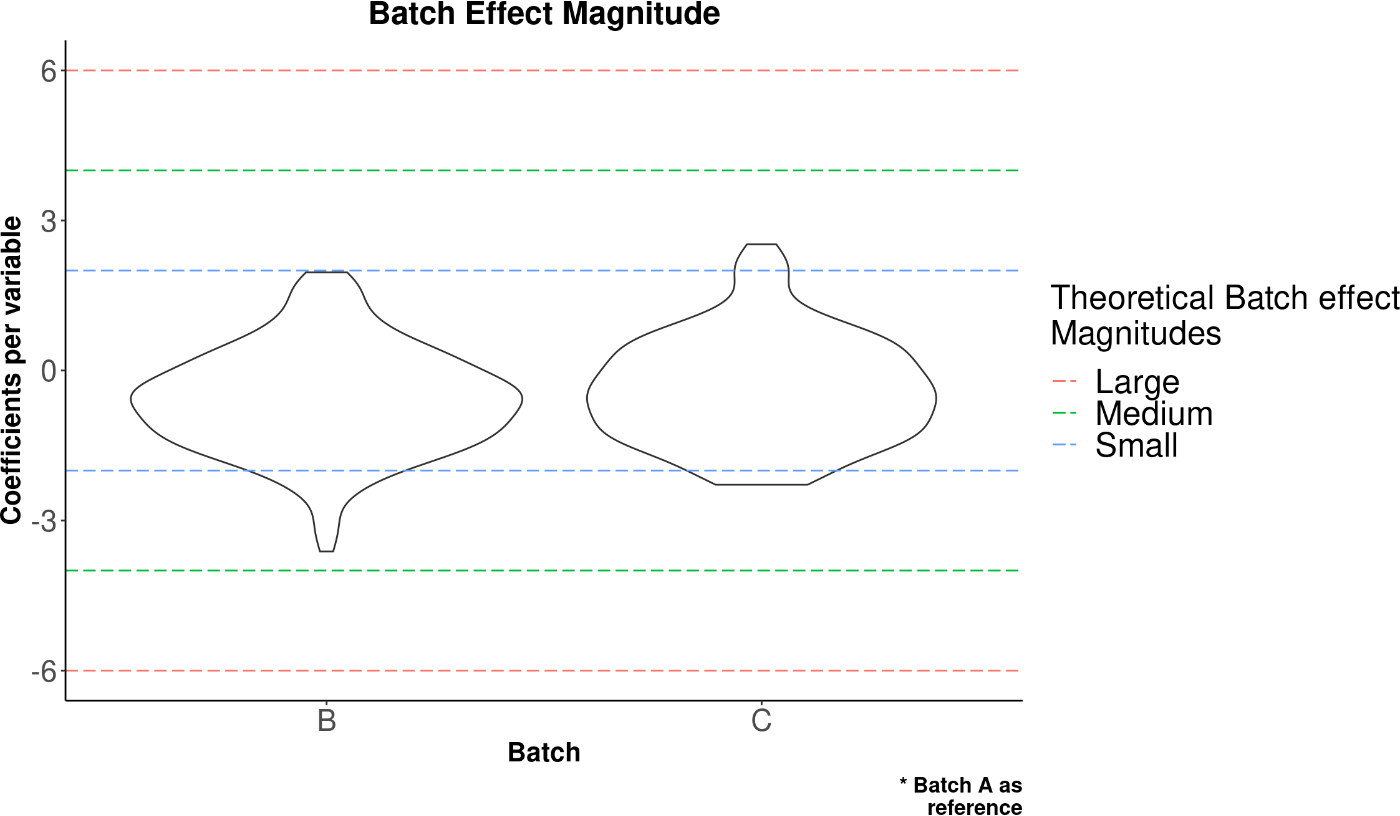
图9：批次效应估计图

虚线表示理论批次效应幅度。小提琴图表示数据中观察到的批次效应系数的分布。
酵母例子的理论批次效应幅度在图 9 中展示。小提琴图展示了变量空间中批次效应系数的分布情况（对于RNA-seq数据而言，这些变量是基因）。具有较高值的系数对应于对批次效应的存在贡献最大的那些变量，因此，当分布接近零时，批次效应较低。尽管在小至中等批次效应幅度下，MultiBaC的修正性能已经过测试和验证，但在大批量效应下其性能有所下降。相比之下，ARSyN受批次效应幅度的影响并不大。
以下是PCA图表的中文翻译。

PCA图

可以通过比较修正前后的PCA图来评估ARSyNbac或MultiBaC修正的效果。对于MultiBaC，只有在所有组学数据矩阵共享相同的变量空间时，才能生成这种图。在我们提供的酵母示例中，每种组学数据类型都是以基因相关信息的形式获得的，因此可以将矩阵按变量（基因）合并，进行PCA分析。
这些PCA图对于ARSyNbac输出的示例可以在ARSyN部分找到。这里我们演示了如何生成和解释它们以进行MultiBaC校正。在原始数据上的PCA（图10：【链接】）和校正数据上的PCA（图11：【链接】）是使用plot函数获得的，分别使用“typeP = pca.org”或“typeP = pca.cor”。

plot (my_final_mbac, typeP = “pca.org”,
cex.axis = 1, cex.lab = 1, cex = 3, bty = “L”,
cex.main = 1.2, pch = 19)

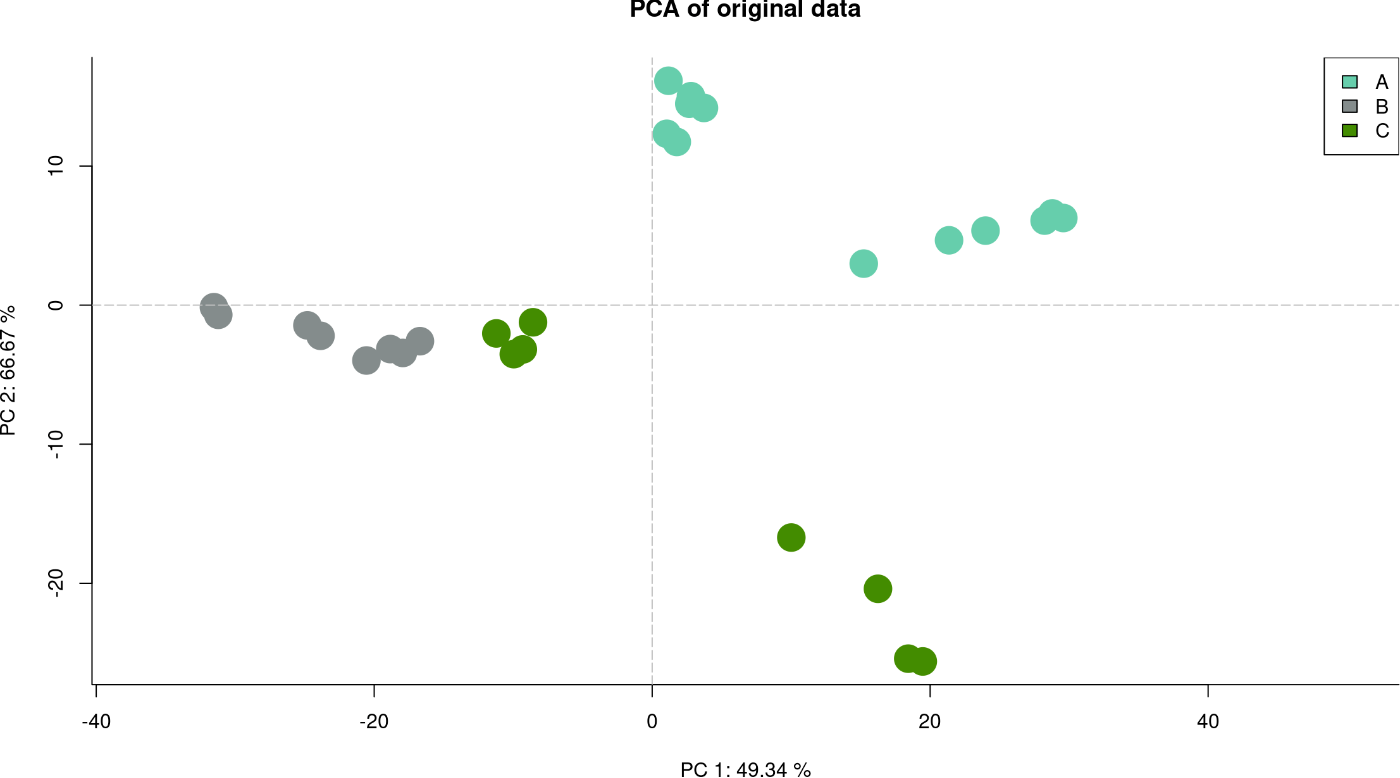
图10：在原始数据上执行PCA得到的主成分图

plot (my_final_mbac, typeP = “pca.cor”,
cex.axis = 1, cex.lab = 1, cex = 3, bty = “L”,
cex.main = 1.2, pch = 19)

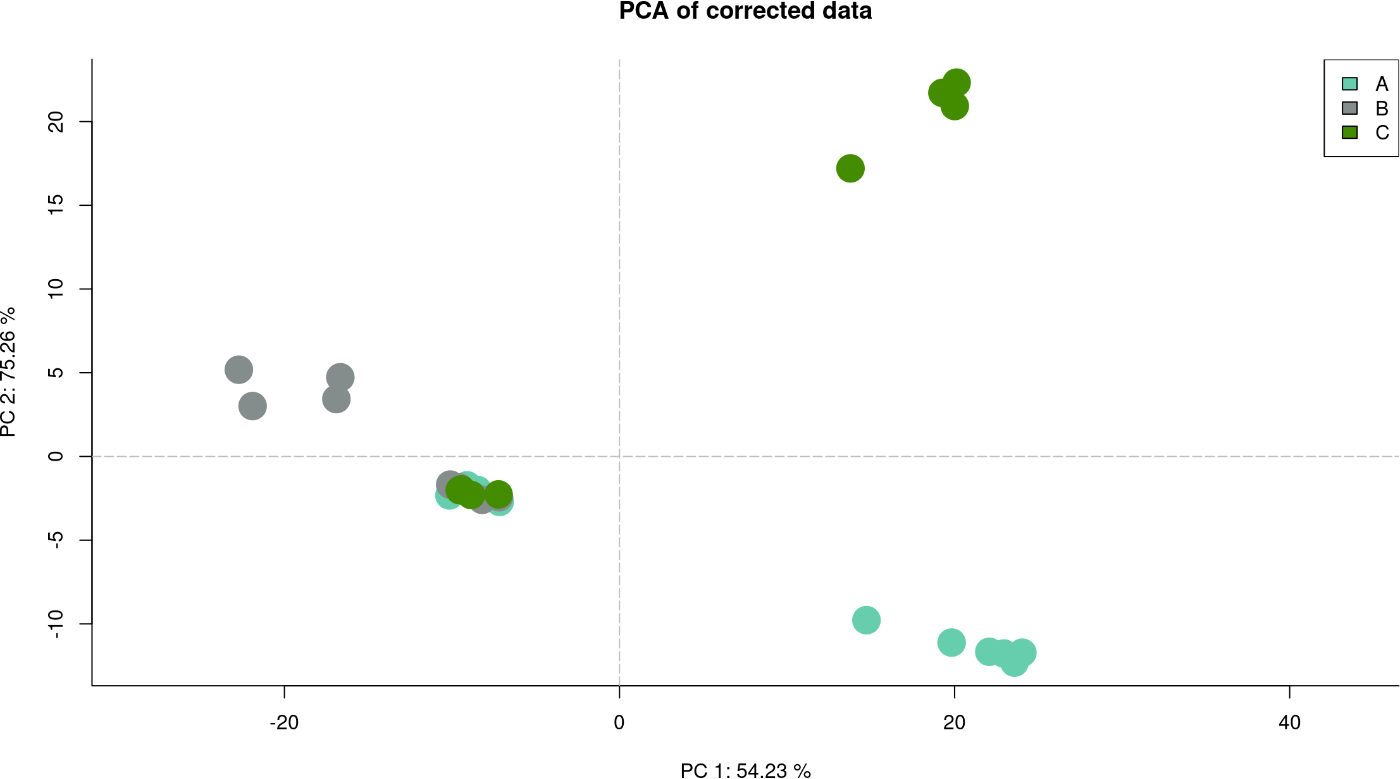
图11：修正数据上的主成分分析（PCA）图（默认设置）
默认情况下，此函数使用随机颜色表示每个组（默认情况下是批次）。然而，同时显示实验因素信息会很有用。为此，我们建议使用自定义的col.per.group和pch参数。图12中给出了一个示例，使用typeP = pca.both同时显示两个PCA图。我们还可以使用comp2plot参数绘制多个组件，以指示所需数量。用户还可以使用两个参数添加自定义图例：legend.text和args.legend。通过legend.text，我们指示图例的文本标签，其余图例参数保存在args.legend（x，y，pch，fill，col，bty等)中。如果向函数提供legend.text，则不考虑args.legend。

custom_col <- c(“brown2”, “dodgerblue”, “forestgreen”)
custom_pch <- c(19,19,19,1,1,1,15,15,15,0,0,0, # batch A
19,19,1,1,17,17,2,2, # batch B
19,19,1,1,18,18,5,5) # batch C

plot(my_final_mbac, typeP = “pca.both”, col.by.batch = TRUE,
col.per.group = custom_col, comp2plot = 1:3,
cex.axis = 1.3, cex.lab = 1.2, cex = 3, bty = “L”,
cex.main = 1.7, pch = custom_pch,
legend.text = c(“Color”, names(my_final_mbac$ListOfBatches),
“Shape”, c(“RNA”, “GRO”, “RIBO”, “PAR”),
“Fill”, levels(colData(my_final_mbac$ListOfBatches$A)$tfactor)),
args.legend = list(“x” = “topright”,
“pch” = c(NA, 15, 15, 15,
NA, 19, 15, 17, 18,
NA, 19, 1),
“col” = c(NA, “brown2”, “dodgerblue”, “forestgreen”,
NA, rep(1, 4),
NA, 1, 1),
“bty” = “n”,
“cex” = 2))

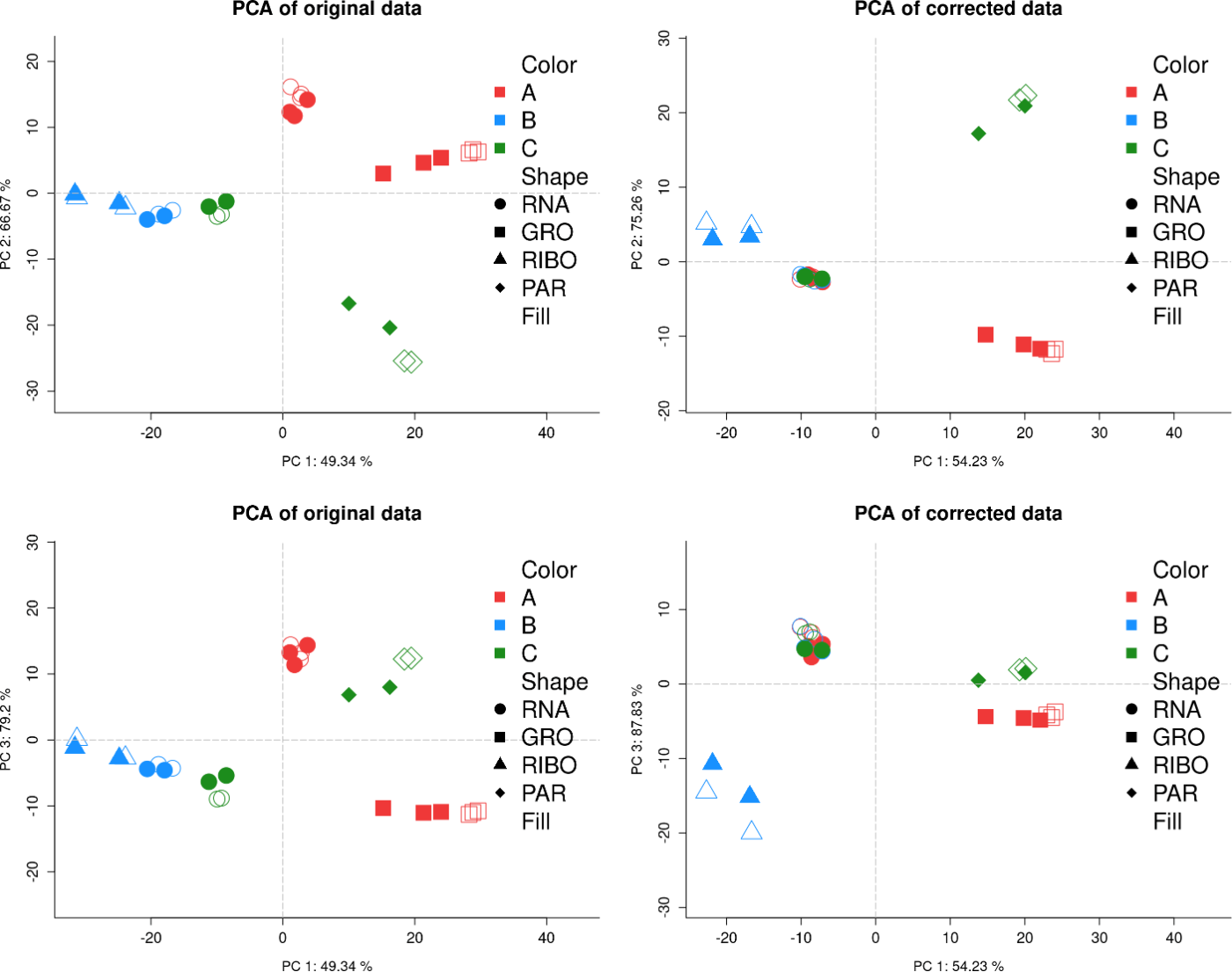
图12：定制的主成分分析图
原始数据（左侧面板）和修正数据（右侧面板）。上图显示第二主成分（PC）与第一主成分的关系，而下图则显示第三主成分与第一主成分的关系。
在这种情况下，批次效应校正可在通用数据（RNA-seq、点）中观察到。当通用数据放在一起后，批次效应已被移除，并且在校正后，这些成分（尤其是第二和第三成分)会根据实验条件对通用数据进行分离，而不是根据批次进行分离。如图例所示，点的形状表示 omic数据类型，然而批次效应校正仅在通用数据中可见。

总结

MultiBaC是用于多组学和隐藏批次效应场景中的批量效应去除工具。该包提供多种图形输出，用于模型验证和批量效应校正评估。快和小果一起用MultiBaC R包更有效地处理多组学实验中的批量效应问题，从而提高数据分析的准确性和可靠性吧！

参考文献

1. Nueda MJ, Ferrer A, Conesa A. ARSyN: A method for the identification and removal of systematic noise in multifactorial time course microarray experiments. Biostatistics. 2012;13:553–66.
2. Pelechano V, Pérez-Ortín JE. There is a steady-state transcriptome in exponentially growing yeast cells. Yeast. 2010;27:413–22. doi:10.1002/yea.1768.
3. García-Martínez J, Aranda A, Pérez-Ortín J. Genomic run-on evaluates transcription rates for all yeast genes and identifies gene regulatory mechanisms. Molecular Cell. 15:303–13. doi:10.1016/j.molcel.2004.06.004.
4. Pelechano V, Chávez S, Pérez-Ortín JE. A complete set of nascent transcription rates for yeast genes. PloS one. 5:e15442; e15442–2. doi:10.1371/journal.pone.0015442.
5. Zid BM, O’Shea EK. Promoter sequences direct cytoplasmic localization and translation of mRNAs during starvation in yeast. Nature. 514:117–21. doi:10.1038/nature13578.
6. Freeberg MA, Han T, Moresco JJ, Kong A, Yang Y-C, Lu ZJ, et al. Pervasive and dynamic protein binding sites of the mRNA transcriptome in saccharomyces cerevisiae. Genome biology. 14:R13–3. doi:10.1186/gb-2013-14-2-r13.

如果小伙伴有其他数据分析需求，可以尝试使用本公司新开发的生信分析小工具云平台，零代码完成分析，非常方便奥，云平台网址为：(http://www.biocloudservice.com/home.html)，其中也包括了通路表达分析(http://www.biocloudservice.com/313/313.php)，单细胞的基因共表达分析(http://www.biocloudservice.com/906/906.php)等各种小工具哦~，有兴趣的小伙伴可以登录网站进行了解。