生信数据处理基础中的精华SVD:SVD奇异值分解在降维中的无限魅力!
点击蓝字
关注我们
大家在学习线性代数时都应该听说过SVD奇异值分解,这是一种常用的矩阵分解技术。但是你们知道在生物信息学中,SVD奇异值分解也被广泛应用于数据降维吗?在基因表达数据的分析中,数据通常是高维的,而这些高维数据往往很难可视化或者解释。因此,需要对数据进行降维。
今天小师妹就用SVD奇异值分解来对tissuesGeneExpression组织基因表达数据进行降维操作~该数据中共有样本189个,基因22,215个。
奇异值分解(Singular Value Decomposition,简称SVD)是一种重要的矩阵分解方法。它可以将一个矩阵分解为三个矩阵的乘积,其中包括左奇异向量矩阵U、奇异值矩阵D和右奇异向量矩阵V。这种分解方法不仅可以用来降低矩阵的维度,同时也可以用来提取矩阵的主要特征。其中U和V都是正交矩阵,而D是对角矩阵。对角矩阵D的对角线上的元素就是奇异值,奇异值按照大小顺序排列,奇异值越大,其包含的方差(也可以理解为信息)则越大。
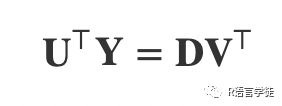
在SVD中,奇异值代表了矩阵的重要特征,而奇异向量则代表了这些特征所在的方向。通过计算奇异值的数量及其对应的奇异向量,我们可以生成一个可以近似代替原矩阵的矩阵,而且近似矩阵具有更低的维度,从而实现了数据降维的目的。同时,由于奇异值是按照大小排列的,所以我们可以对其进行截断,舍弃不重要的特征向量,从而进一步提高数据压缩的效果。
首先我们载入数据以及需要用到的工具包
library(rafalib)library(MASS)# #加载数据library(tissuesGeneExpression)data(tissuesGeneExpression)
从包含基因表达数据的e矩阵中生成500行(基因)的随机样本。Nrow (e)返回e矩阵的行数,sample()随机选择500个行索引(不进行替换)
# #以确保每次运行代码时生成相同的随机数set.seed(1)ind <- sample(nrow(e),500)Y <- t(apply(e[ind,],1,scale))
通过缩放每一行使其平均值为0,标准差为1,对500个随机选择的基因表达数据进行标准化。apply()函数对e[ind,]矩阵的每一行应用scale()函数,t()函数对所得矩阵进行转置,使基因在列中,样本在行中。现在得到的矩阵Y可以进行SVD分析。
使用函数svd( )进行奇异值分解
s <- svd(Y)U <- s$uV <- s$v# #使用diag( )将奇异值转换成对角矩阵D <- diag(s$d)# #Yhat表示使用SVD分解对原始数据矩阵Y的低秩逼近。Yhat <- U %*% D %*% t(V)resid <- Y - Yhatmax(abs(resid))
从原始标准化数据矩阵Y中减去Yhat得到残差矩阵。使用max(abs(resid))计算最大绝对残差,它表示原始数据矩阵Y与其低秩近似Yhat之间的最大偏差。残差可以用来评估近似的质量,并确定在低秩近似中保留的适当的奇异值的数量。
plot(s$d)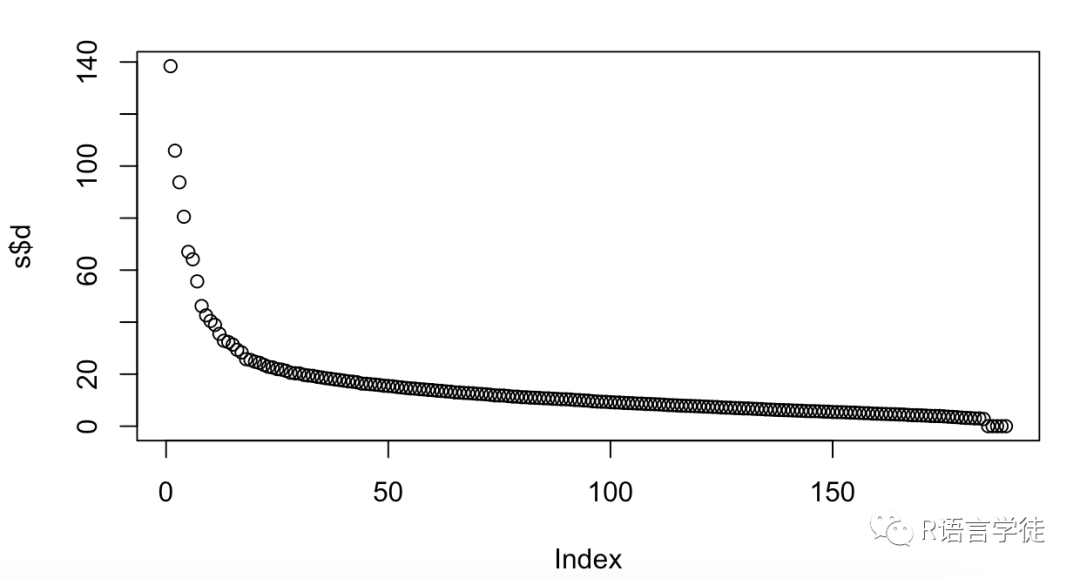
该图将按降序显示奇异值的值。x轴按降序表示奇异值的索引。也就是说,x轴上的第一个点表示第一个(最大)奇异值,第二个点表示第二大奇异值,依此类推。y轴表示奇异值的大小。
一个典型的奇异值图会显示奇异值的大小迅速下降,少数奇异值支配其他奇异值。该图可用于确定在原始数据矩阵的低秩近似中保留的适当数量的奇异值。一般来说,我们希望保留足够的奇异值来捕获数据中的大部分变化,但不要太多,以免近似过于复杂。
确定奇异值的适当数量的一种常用方法是在图中寻找一个“弯头”,在那里奇异值的大小迅速下降。肘部左侧的奇异值个数可以保留在低秩近似中,而剩余的奇异值可以设为零。另外,一种更定量的方法是使用基于保留的奇异值捕获的总变化的阈值。
plot(s$d^2/sum(s$d^2)*100,ylab="Percent variability explained")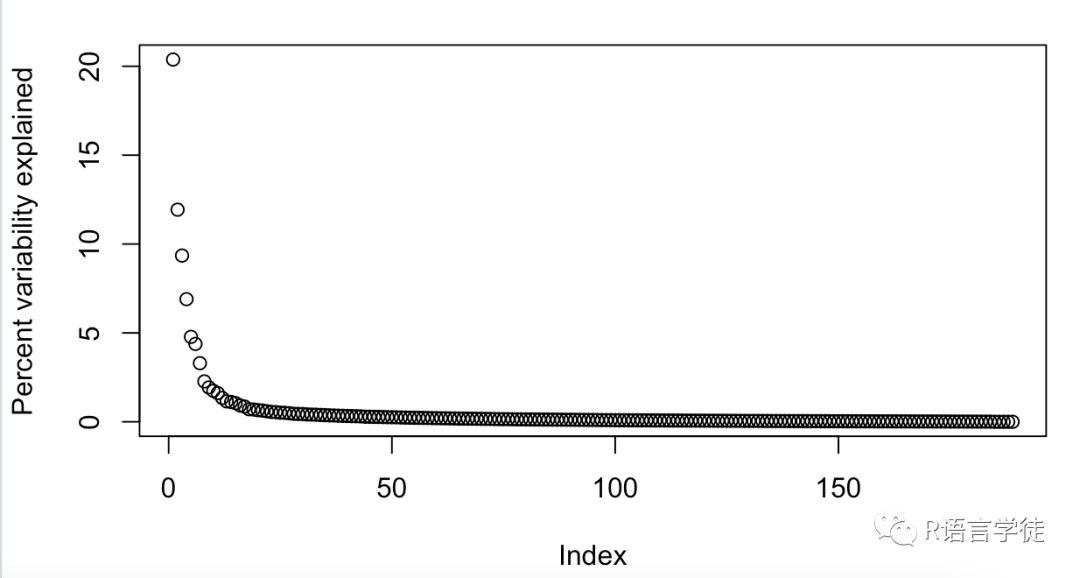
这个图像表示了每个奇异值包含了百分之多少的信息。
我们也可以通过累积图像来查看

可以看到,我们保留前30个特征,就能保留原始信息的80%,保留前100个就可以几乎保留所有信息,要知道我们的原始维度可是189个特征哦!
我们可以查看一下保留一半特征时候的情况
k <- 95 ##out a possible 189Yhat <- U[,1:k] %*% D[1:k,1:k] %*% t(V[,1:k])resid <- Y - Yhatboxplot(resid,ylim=quantile(Y,c(0.01,0.99)),range=0)var(as.vector(resid))/var(as.vector(Y))

boxplot()函数用于可视化残差的分布,残差表示原始数据矩阵与低秩近似之间的偏差。ylim参数将图的y轴限制设置为原始数据矩阵的第1和第99个百分位数,而range参数控制箱线图的晶须长度。
比值var(as.vector(ressid))/var(as.vector(Y))表示原始方差中未被低秩近似解释的比例。换句话说,它测量的是在近似过程中丢失的信息量。这里我们丢弃了一半的特征,但是只丢失了3%的信息。
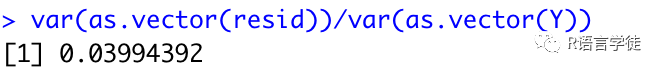
通过这个例子,我们可以看到SVD奇异值分解虽然是基础的线性代数知识,但是在生物信息分析的降维应用中也是非常不错的选择~下一节,小师妹将给大家带来以SVD为基础的多维尺度变换(Multi-Dimensional Scaling),各位敬请期待~
更多实用方便的小工具在云生信平台等着你哦~
http://www.biocloudservice.com/home.html
E
N
D

