3分钟掌握生物学相关性分析中的各种变量和检验
点击蓝字,关注我们
相信各位小伙伴在对各种生物学数据变量(年龄,性别,基因突变频率……)进行相关性分析时,都被t检验,wilcoxon检验,kruskal-wallis检验,ANOVA方差分析,卡方检验等等各种差异检验弄得焦头烂额。接下来小师妹就为大家系统性地总结了在不同类型变量下,到底该用哪一种相关性分析,看了小师妹的教程,大家以后在对这些数据进行相关性分析时就可以轻松拿捏。后续小师妹会带来R语言上代码分析和绘图的教学~
首先小师妹先介绍一下连续变量到底是什么:在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值。例如年龄和体重就是两个连续变量,这时候就可以用我们上面的方法。下面是进行检验的数据格式:

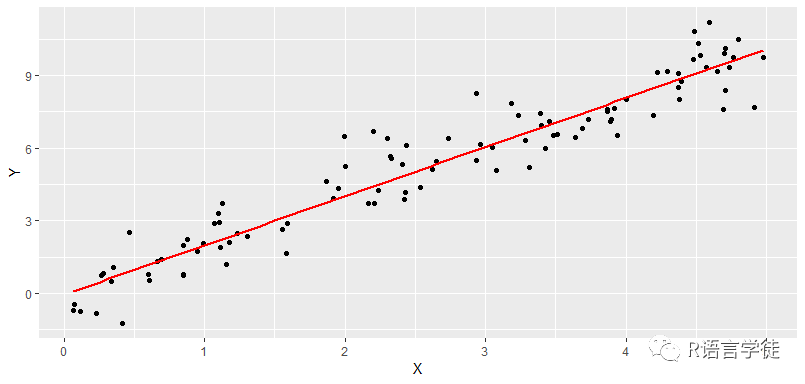
这是肿瘤大小和体重的相关性分析。
两个连续变量之间的线性相关关系可以采用“简单相关分析”,也就是用线性相关来拟合,用Pearson相关系数或Spearman相关系数进行表示。
离散变量则是指变量值可以按一定顺序一一列举,通常以整数位取值的变量,例如企业的个数、企业的职工人数、企业的机器台数、在校学生人数等。但是离散变量中又有一类比较特殊的是分类变量,只能被分为不同类别,而无法用数值尺度来记录的变量,例如性别,颜色等。下面是进行检验时数据的格式:

这是性别和肿瘤大小进行相关性分析的例子。
当遇到连续变量和离散变量的相关性分析时就有点伤脑筋了,这时候我们主要使用的是t检验,ANOVA方差分析,wilcoxon检验,kruskal-wallis检验这四种差异检验方法,具体什么情况下用,再多的话也可能说不清楚,小师妹整理了一个表格,大家一看就立刻明白了。
这里涉及到了参数检验和非参数检验,小师妹来解释一下:参数检验是基于样本的观测数据对总体参数(比如总体均值、方差)及总体参数差异性的检验,要求连续变量符合一定的分别,在我们的生物学数据中主要是符合正态分布;非参数检验不要求变量符合正态分布,是通过样本数据对总体分布形态等特征进行推断的统计检验方法。
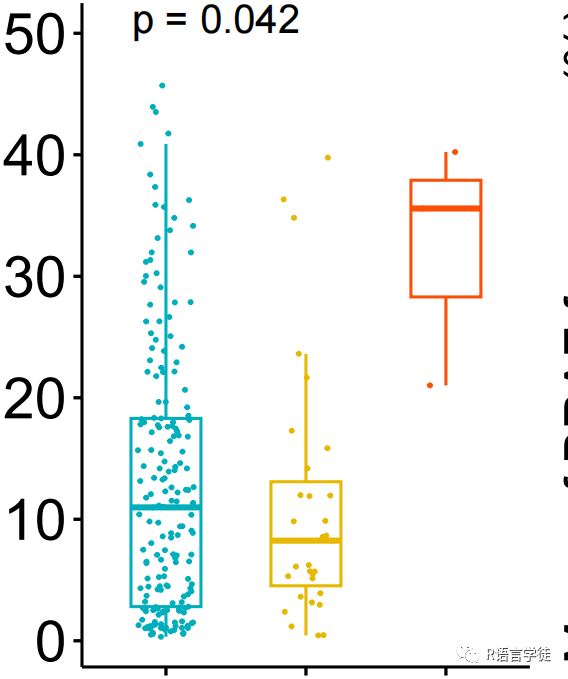
这类检验绘图主要是绘制箱线图,加上散点,后续小师妹会为大家带来代码的。
当离散变量和离散变量进行相关性分析时,例如性别和某个基因是否有突变的相关性分析时,我们就要用到卡方检验和Fisher’s 精确检验了。下面是进行检验时数据的格式:

这是性别和BRAF是否发生突变的相关性分析。
这两者是有区别的,接下来小师妹就来详细叙述一下二者的区别。理论上来说,Fisher精确检验得到的结果才是准确的,卡方检验是利用了大样本下渐近卡方分布的性质,属于非参数检验,即使是近似服从卡方分布,得到的结果仍是近似值。Fisher精确检验本质上是一种基于超几何分布理论可直接计算概率的检验方法。简单来说,样本数大时用卡方检验,样本数小时用Fisher精确检验。
这类检验的绘图一般我们都是采用柱状图或者饼图:

横坐标代表一个离散变量,堆叠的不同颜色的柱子代表另一个离散变量。
最后小师妹要说一个大家学习过程中可能会疑惑的问题。当我们遇到离散变量具有许多水平,那么最好将其视为连续变量,例如人数,肿瘤的个数等等,这些变量理论上来说都是离散变量,但具有很多个水平,因此进行相关性分析时,最好将其视为连续变量进行分析。
这就是本次小师妹分享的全部内容,后续小师妹将为大家带来R语言上的分析和绘图教程。
★

