R语言也能接入lingo?线性规划包之lpSolve
点击蓝字
关注我们
大家好,今天小师妹要向大家介绍的是优化理论中最为基础但也最为实用的优化领域——线性规划问题。

在我们的生物信息学和计算生物学中,通常会涉及到一系列重要的优化问题,这些问题需要找到最小化或最大化某个特定目标函数的解决方案。在大部分情况下,这些问题是组合优化问题,可以表述为整数线性规划问题。如”de novo肽段测序问题”,它涉及到仅通过肽段的串联质谱图而不依赖于基因组数据库或蛋白质数据库中的额外信息来识别肽段的序列。这个问题可以被表述为一个图论问题,要求计算有向无环图中最长反对称路径的计算。再如RNA-Seq数据的”异构体推断和丰度估计问题”。这个问题涉及到预测一组表达的RNA异构体,即与不同的剪接变异相关的全长RNA转录本,以及它们各自表达水平的估计。我们应用了一种称为”延迟列生成”的线性规划技术,它允许我们扩展搜索空间,而不必显式枚举可能庞大的候选异构体集合。因此,我们的方法允许识别那些由于不完整的读取覆盖而无法恢复的异构体。延迟列生成算法的一个核心组成部分是一个整数线性规划制定。
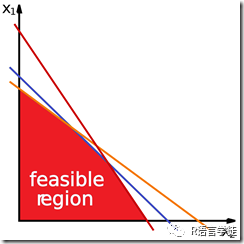
作为常见的线性规划问题,它是数学和运筹学领域的一个重要分支,通常用于优化问题的解决。它的主要目标是在一组线性约束条件下,找到一个线性目标函数的最优解。线性规划可以用于多种应用领域,包括生产计划、资源分配、运输问题、投资组合优化等等。
线性规划的一般形式如下:最大化:为约束条件:变量限制:
其中, 是一个包含目标函数系数的向量, 是我们要优化的决策变量向量, 是包含约束条件系数的矩阵, 是约束条件的右侧向量。线性规划的目标是找到变量向量 的值,使得目标函数 最大化,同时满足约束条件。
线性规划可以使用不同的数学工具和算法来求解,如单纯形法、内点法等。而在计算机软件中,我们可以通过R语言进行编写程序求解。小师妹将分别带大家使用R中的lpSolve包和lpSolveAPI包,我们可以通过在lpSolve::lp函数中设置参数“all.int=TRUE”来设置所有变量都应该是整数。当然,lpSolve可以处理整数和实数。大家一定要认真阅读和学习哦!
定义问题、编写函数
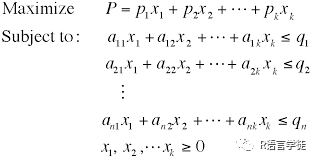
首先,我们需要用数学的方式来解释这个问题。让我们定义以下变量
-
是要生产的 4P 椅子的数量。
-
是要生产的 3P 椅子的数量。
-
是要购买的木块数量。
现在我们可以定义 作为决策变量向量。注意,它必须是。
我们希望最小化总成本,因此我们必须将目标函数设置如下
成本 (成本)
这意味着 。
可以通过以下方式设置约束
-
座位
-
对于腿
-
对于背面
-
生产的椅子的最低数量
我们现在可以定义系数矩阵
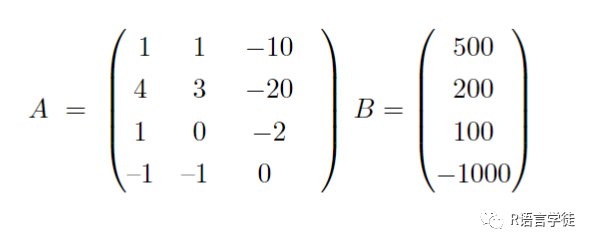
我们需要最小化目标函数(由C表示),同时满足约束条件(由A、B和constranints_direction表示)。
现在,我们开始编写程序,我们的目标是找到一组决策变量,以最小化一个线性目标函数,同时满足一组线性约束条件。具体来说:
-
定义决策变量的系数向量 C,该向量表示目标函数中每个决策变量的系数。
-
创建一个约束矩阵 A,该矩阵包含了线性约束条件的系数。每行代表一个约束条件,每列代表一个决策变量。
-
定义约束条件的右侧向量 B,表示每个约束条件的限制值。
-
定义约束方向向量 constranints_direction,指示每个约束是小于等于(”<=”)还是大于等于(”>=”)。
#导入R包并定义函数install.packages("lpSolve")library(lpSolve)## 设置决策变量的系数 -> CC <- c(30, 40, 80)# 创建约束矩阵 BA <- matrix(c(1, 1, -10,4, 3, -20,1, 0, -2,1, 1, 0), nrow=4, byrow=TRUE)# 约束条件的右侧B <- c(500, 200, 100, 1000)# 约束方向constranints_direction <- c("<=", "<=", "<=", ">=")
通过lp函数进行求解
接下来,通过lpsolve中的lp函数进行问题的求解,使用lp函数进行线性规划求解,direction=”min”表示要最小化目标函数。objective.in包含目标函数的系数,const.mat包含约束矩阵,const.dir包含约束方向,const.rhs包含约束右侧的值。all.int = T 表示要求解整数线性规划问题。
最优解将存储在optimum变量中,可以从中获取最小化的目标函数值以及对应的决策变量值。
# 寻找最优解optimum <- lp(direction="min",objective.in = C,const.mat = A,const.dir = constranints_direction,const.rhs = B,all.int = T)
输出问题的解
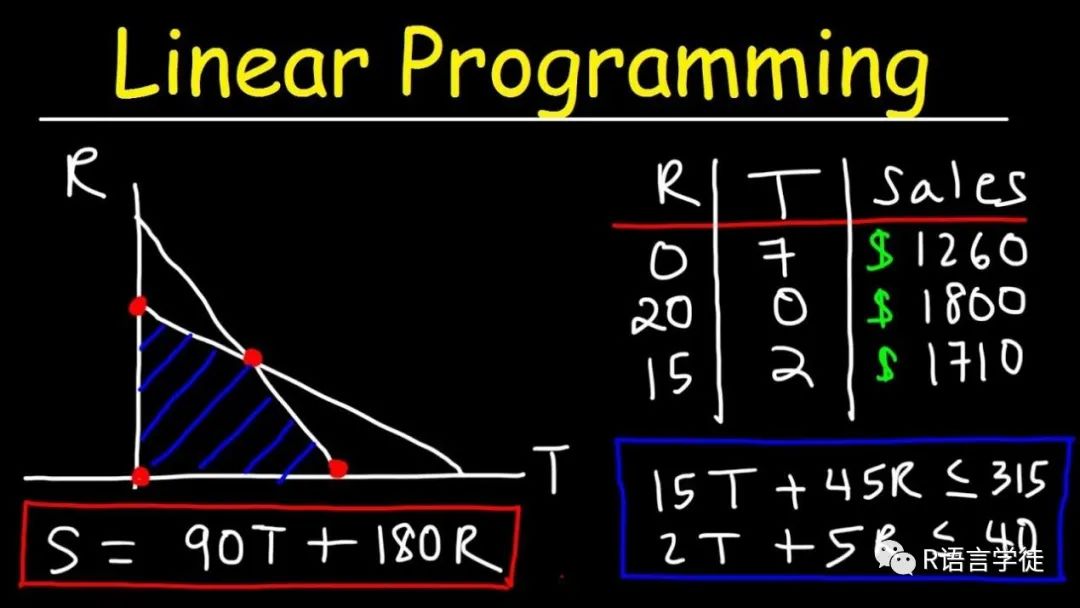
既然我们已经求解出目标函数的最优解,那么下面的问题就是如何获得这个最优解,让小师妹向大家演示一遍。
# 打印状态: 0 = 成功, 2 = 无可行解print(optimum$status)# 显示 x_4p、x_3p 和 x_w 的最优值best_sol <- optimum$solutionnames(best_sol) <- c("x_4p", "x_3p", "x_w")print(best_sol)# 检查最优点处目标函数的值print(paste("总成本: ", optimum$objval, sep=""))
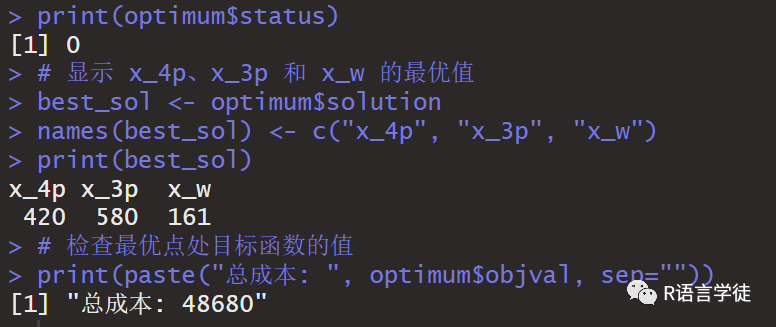
显然,我们可以得到总成本的最小值为48680,此时的
使用lpSolveAPI包进行求解
我们还可以通过lpSolveAPI包进行线性规划问题的求解,该包相对lpSolve可能略微复杂,但具有更清楚明确的定义。
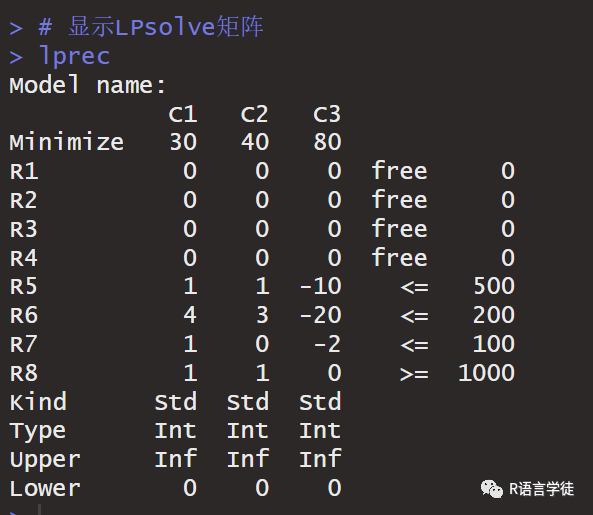
# 使用lpSolveAPI进行问题求解install.packages("lpSolveAPI")require(lpSolveAPI)# 设置4个约束和3个决策变量lprec <- make.lp(nrow = 4, ncol = 3)# 设置我们要解决的问题类型为最小化lp.control(lprec, sense="min")# 设置决策变量类型为整数set.type(lprec, 1:3, type=c("integer"))# 设置目标函数的系数向量 Cset.objfn(lprec, C)# 添加约束add.constraint(lprec, A[1, ], "<=", B[1])add.constraint(lprec, A[2, ], "<=", B[2])add.constraint(lprec, A[3, ], "<=", B[3])add.constraint(lprec, A[4, ], ">=", B[4])# 显示LPsolve矩阵lprec# 解决问题solve(lprec)# 获取决策变量的值get.variables(lprec)# 获取目标函数的值get.objective(lprec)# 注意:决策变量的默认边界为 c(0, 0, 0) 和 c(Inf, Inf, Inf)get.bounds(lprec)# 边界可以使用以下函数设置# lpSolveAPI::set.bounds()
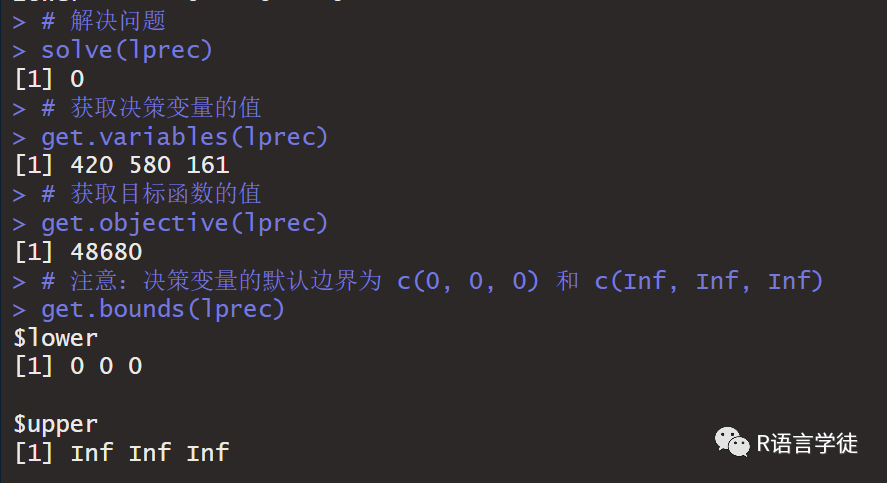
那么最后,使用lpSolve包和lpSolveAPI包进行线性规划问题的定义和求解小师妹就向大家教学完毕啦,是不是非常easy呢,希望小伙伴们课下对多学习哦。相信小伙伴们已经基本掌握了这两种求解线性规划的R包,会通过R语言编写相应的程序。到这里线性规划问题就基本完结啦。小师妹要和大家说再见咯,一定要自己练习一下哦,同时如果大家想要继续了解更多有关R语言内容可以持续关注小师妹哦~~或者也可以关注我们的官网也会持续更新的哦~ http://www.biocloudservice.com/home.html


