数据降维,不得不说的经典机器学习方法——PCA
生信人R语言学习必备
立刻拥有一个Rstudio账号
开启升级模式吧
(56线程,256G内存,个人存储1T)

信息过度复杂是多变量数据最大的挑战之一。许多小伙伴经常会遇到这种问题,于是我们会考虑用降维来解决,这时候很多人都会想到PCA降维,那么PCA到底是什么呢?今天小果来带大家探索PCA算法的原理。
PCA(Principal Component Analysis)全称为主成分分析,是一种无监督的数据降维方法,通过主成分分析可以尽可能保留下具备区分性的低维数据特征。主成分分析图能帮助我们直观地感受样本在降维后空间中的分簇和聚合情况,这在一定程度上亦能体现样本在原始空间中的分布情况。
相信大家看到这里应该大致能知道PCA究竟能干嘛了,那么该怎么实现呢?别着急,小果下面通过一个分析过程来带大家学习具体流程。
1、载入数据及相关R包
library(ggplot2)data <- subset(iris, select = -Species)class = iris[["Species"]]
2.PCA分析
#进行主成分分析pca = prcomp(data, center = T, scale. = T)#保存各个样本主成分的数据pca.data = data.frame(pca$x)pca.variance = pca$sdev^2 / sum(pca$sdev^2)
3.主成分选取
#查看主成分分析的详细情况summary(pca)#执行后会得到如下结果
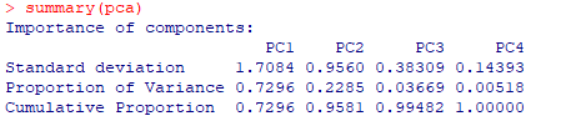
说明:结果中的PC1、PC2、PC3、和PC4是计算出来的主成分,图中的Standard deviation代表每个主成分的标准差,Proportion of Variance代表每个主成分的贡献率,Cumulative Proportion代表各个主成分的累积贡献率。每个主成分都不属于X1、X2、X3和X4中的任何一个。第一主成分、第二主成分、第三主成分和第四主成分都是X1、X2、X3和X4的线性组合,也就是说最原始数据的成分经过线性变换得到了各个主成分。一般地,选择累积贡献率达到八成的前几个主成分即可(这个实例中我们选择前两个,毕竟第二主成分的贡献率也比较大)。
4.PCA可视化
#自定义颜色palette = c("mediumseagreen", "darkorange", "royalblue")#绘制PCA选取特征下样本散点图ggplot(pca.data, aes(x = PC1, y = PC2, color = class)) +geom_point(size = 3) +geom_hline(yintercept = 0) +geom_vline(xintercept = 0) +stat_ellipse(aes(x = PC1, y = PC2), linetype = 2, size = 0.5, level = 0.95, inherit.aes = FALSE) +theme_bw() +scale_color_manual(values = palette) +theme(panel.grid.major.x = element_blank(),panel.grid.minor.x = element_blank(),panel.grid.major.y = element_blank(),panel.grid.minor.y = element_blank()) +labs(x = paste0("PC1: ", signif(pca.variance[1] * 100, 3), "%"), y = paste0("PC2: ", signif(pca.variance[2] * 100, 3), "%"), title=paste0("PCA of iris"))+theme(plot.title = element_text(hjust = 0.5))
分析最后我们会得到一个PCA分析图,如下图1所示,图中的横纵坐标分别对应主成分PC1和PC2,整体表现了所有样本在这两个主成分上的分布。同时小伙伴们还可以保存样本在主成分上的表达水平来开展其他分析,具体样例如图2所示,每行为一个样本,列为不同的主成分。
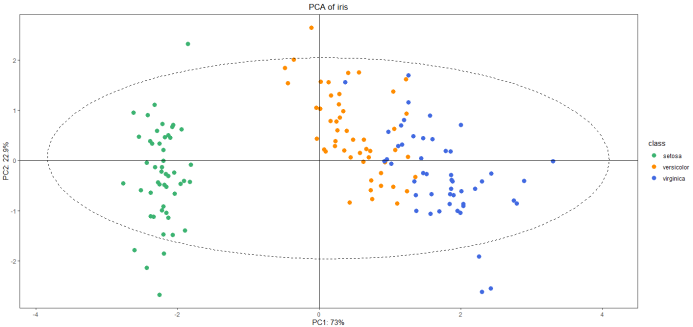
图1 主成分分析图
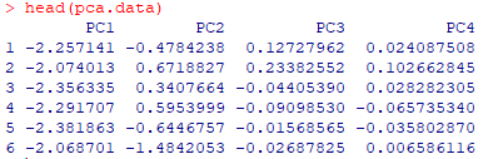
图2 样本主成分表达矩阵样例
大功告成!分析到这里就结束了,相信大家已经掌握了,感兴趣的小伙伴快去试试吧!
这里推荐一下小果新开发的零代码云生信分析工具平台包含超多零代码小工具,上传数据一键出图,感兴趣的小伙伴欢迎了解~
网址:http://www.biocloudservice.com/home.html
今天小果的分享就到这里,欢迎大家和小果一起讨论学习,下期再见哦!
小果友情推荐
好用又免费的工具安利


