数据存在批次效应?来这里让大海哥教你怎么处理
点击蓝字 关注我们
大家好,我是大海哥,今天大海哥给大家带来的不同于以往只是简单的技术分享,今天要分享的更是我们追求科研真实性路上的一个重要方法,没错,就是数据批次效应。那么很多不了解的小伙伴就要问了,数据批次效应是什么呢?大海哥先来给大家介绍一下其原理。
批次效应(Batch Effect)是在实验设计和高通量实验数据分析中常见的一个概念,它指的是同一实验中的不同批次(或者来源、时间、实验条件等不同因素)之间引入的系统性变异。这些批次效应可能会对实验结果的解释和数据分析造成干扰,因为它们可能掩盖了与感兴趣因素无关的变异,从而导致误解。批次效应在基因表达分析、蛋白质组学、代谢组学等高通量数据研究中特别常见。
主要的批次效应可能包括:
技术批次效应:
这种效应源自于实验设备、试剂、操作者等技术因素的差异,可能会导致数据在不同批次之间产生变异。
生物批次效应:
这种效应可能是由于实验样本来源的变化,如不同的动物个体、人体样本、细胞系等,以及实验环境的变化,如温度、湿度等,引起的系统性变异。
时间批次效应:如果实验在不同时间点进行,可能会引入时间相关的变异,如季节性变化、生长阶段变化等
数据处理批次效应:
在数据分析过程中,如果采用了不同的数据处理方法、参数或软件工具,也可能导致批次效应。
今天,大海哥就要对存在批次效应的基因表达数据进行处理,让他们可以完美融合!
今天,大海哥就要对存在批次效应的基因表达数据进行处理,让他们可以完美融合!
#首先,我们下载一下对应的数据#我们选择GEO数据的两个存在批次效应的数据哦!rm(list = ls())options(stringsAsFactors = F)library(GEOquery)eSet1 <- getGEO("GSE83521",destdir = '.',getGPL = F)#(1)提取表达矩阵expexp1 <- exprs(eSet1[[1]])exp1[1:4,1:4]dim(exp1)#然后我们看一下这个数据的箱型图# 一定要看boxplotboxplot(exp1,las=2)

pd1 <- pData(eSet1[[1]])#(3)提取芯片平台编号gpl1 <- eSet1[[1]]@annotation#然后开始下载第二个数据eSet2 <- getGEO("GSE89143",destdir = '.',getGPL = F)#(1)提取表达矩阵expexp2 <- exprs(eSet2[[1]])exp2[1:4,1:4]dim(exp2)boxplot(exp2,las=2)
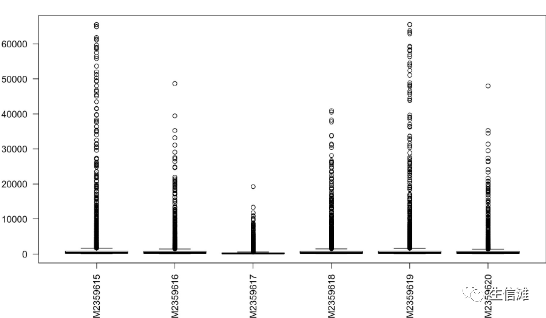
#从上面的箱线图结果可以看到,数值的表达量并不在同一条水平线上,并且有成败上千,也有零,很明显是没有经过log的。这是需要把数据log后再用boxplot来看数据的分布#log(x+1)预处理一下exp2 = log2(exp2+1)boxplot(exp2,las=2)

#然后我们再使用一个厉害的函数normalizeBetweenArrayslibrary(limma)exp2=normalizeBetweenArrays(exp2)boxplot(exp2,las=2)

#可以看到,现在数据集2的数据都基本上处于统一范围区间了,可以进行下一步操作了#探针注释#这一步也是我们日常使用GEO数据必须要有的操作,这里也顺便介绍一下吧#(2)提取临床信息pd2 <- pData(eSet2[[1]])#(3)提取芯片平台编号gpl2 <- eSet2[[1]]@annotationgpl2gpl1#是同一个平台!很不错if(T){library(GEOquery)gpl<- getGEO('GPL19978', destdir=".")dim(gpl)colnames(Table(gpl)) #查一下列明head(Table(gpl)[,c(1,2)])ids=Table(gpl)[,c(1,2)]ids <- ids[-c(1:2),]ids <- ids[-c(1:13),]save(ids,file='ids.Rdata')}
#看一下对应关系
#本次使用的算法是支持lp、distr以及crank,所以上图中对应的指标都支持哦!#同样支持IBS指标,我们看看,一行搞定p$score(msrs("surv.brier"))

#合并数据x1 <- exp1[rownames(exp1) %in% ids$ID,]x2 <- exp2[rownames(exp2) %in% ids$ID,]boxplot(x1,las=2)boxplot(x2,las=2)cg=intersect(rownames(x1),rownames(x2))x_merge=cbind(x1[cg,],x2[cg,])#我们看一下合并后的结果boxplot(x_merge)

#上面这张图,就是非常明显的看到了,由于后面的三个样本就是来自另一个数据集的。所以这种就是说明其存在批次效应#差异分析去除批次效应pd1$titlepd2$characteristics_ch1group_list <- c(rep('tumor',6),rep('normal',6),rep(c('tumor', 'normal'),each=3))gse <- c(rep('GSE83527',12),rep('GSE89143',6))table(group_list,gse)dat <- x_mergelibrary(sva)library(limma)## 使用 limma 的 removeBatchEffect 函数dat[1:4,1:4]batch <- c(rep('GSE83521',12),rep('GSE89143',6))design=model.matrix(~group_list)ex_b_limma <- removeBatchEffect(dat,batch = batch,design = design)dim(ex_b_limma)#这个时候一定要看 boxplot,不然就白看了这么久了!

从上面的图可以看到了,去除了批次效应后,数据的表达水平基本符合正常了,这也说明本次代码实现了我们的目的。大功告成!

点击“阅读原文”进入网址
