亲爱的科研小伙伴们,大家好呀!我是你们的小师妹。今天,我要给大家带来一个超级给力的工具介绍——SNPRelate,一个在基因组学研究中不可或缺的R包。
你是否在面对庞大的基因组数据时感到无从下手?或者在进行全基因组关联研究(GWAS)时,被复杂的计算分析搞得焦头烂额?别担心,今天小师妹就带你一起探索SNPRelate的奥秘,让你的研究工作事半功倍!
首先,我们得知道,GWAS在帮助我们揭示疾病和性状的遗传基础方面发挥着巨大作用。但是,随之而来的计算挑战也不容小觑。幸运的是,我们有SNPRelate和它的好伙伴gdsfmt,这两个高性能计算R包,它们能在多核对称多处理(SMP)计算机架构上,加速PCA和基于血缘同源(IBD)的亲缘关系分析。
在这个美妙的科研旅程中,小师妹将手把手教你如何使用这些工具,从安装到数据准备,再到复杂的数据分析,每一步都会有详细的指导。无论你是生物信息学的新手,还是希望提高分析效率的资深研究者,相信我,你都会在这次学习中有所收获!要注意的是,这个R包操作占用内存比较大,建议使用服务器哦,欢迎联系小师妹租赁性价比高的服务器~
那么,还等什么呢?快跟小师妹一起,踏上这场基因奥秘探索之旅吧!如果你在操作过程中遇到任何问题,别犹豫,记得联系小师妹哦~
首先,让我们开始安装SNPRelate包和另外需要用到的包:
if (!requireNamespace(“BiocManager”, quietly=TRUE))
install.packages(“BiocManager”)
BiocManager::install(“gdsfmt”)
BiocManager::install(“SNPRelate”)
安装好了之后,记得加载这些必要的库:
library(gdsfmt)
library(SNPRelate)
好啦,大家准备好了吗?让我们现在就启程,一起踏上这场激动人心的数据分析之旅吧!
一、 数据准备
- SNPRelate支持的数据格式
在SNPRelate中,我们主要使用一种高效的基因组数据结构(GDS)文件格式来存储全基因组关联研究(GWAS)中的数据。这种格式特别适合于存储大量的SNP(单核苷酸多态性)基因型数据。
接下来,我们可以使用snpgdsOpen函数来打开一个GDS文件。这个函数会返回一个文件对象,我们可以利用这个对象来读取文件中的数据。GDS文件中的数据变量包括样本ID(sample.id)、SNP ID(snp.id)、SNP位置(snp.position)、染色体信息(snp.chromosome)、SNP等位基因(snp.allele)和基因型数据(genotype)。
- sample.id:每个样本的唯一标识符。
- snp.id:每个SNP的唯一标识符。
- snp.position:每个SNP在染色体上的基础位置。
- snp.chromosome:每个染色体的整数或字符映射。
- snp.allele:SNP的等位基因信息。
- genotype:SNP基因型矩阵。
# 打开一个GDS文件
(genofile <- snpgdsOpen(snpgdsExampleFileName()))
# (genofile <- snpgdsOpen(‘hapmap_geno.gds’)) # 也可以直接使用小师妹提供的文件哦
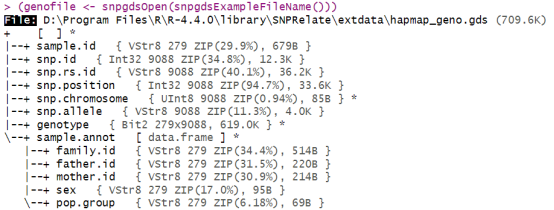
我们可以查看GDS文件中存储了哪些数据。snpgdsSummary函数可以提供文件中基因型的概要信息。
snpgdsSummary(genofile)

我们可以使用read.gdsn函数来获取GDS文件中的特定数据。例如,获取前5个SNP的ID:
# 获取前5个SNP的ID
head(read.gdsn(index.gdsn(genofile, “snp.id”)))

或者获取样本注释信息,比如人口群体信息:
# 读取人口群体信息
pop <- read.gdsn(index.gdsn(genofile, path=”sample.annot/pop.group”))
table(pop)

完成数据读取后,一定要记得关闭GDS文件以释放资源哦!
# 关闭GDS文件
snpgdsClose(genofile)
- 创建GDS文件
snpgdsCreateGeno()函数可以用来创建GDS文件。第一个参数是一个SNP基因型矩阵。输入基因型矩阵中可能存储的值有0、1、2和其他值。“0”表示两个B等位基因,“1”表示一个A等位基因和一个B等位基因,“2”表示两个A等位基因,其他值表示缺失基因型。例如:
# 加载数据
data(hapmap_geno)
# 创建一个gds文件
snpgdsCreateGeno(“test.gds”, genmat = hapmap_geno$genotype,
sample.id = hapmap_geno$sample.id, snp.id = hapmap_geno$snp.id,
snp.chromosome = hapmap_geno$snp.chromosome,
snp.position = hapmap_geno$snp.position,
snp.allele = hapmap_geno$snp.allele, snpfirstdim=TRUE)
# 打开GDS文件
(genofile <- snpgdsOpen(“test.gds”))
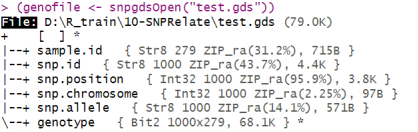
# 关闭GDS文件
snpgdsClose(genofile)
除了上面这种方法,gdsfmt包也可以用来创建GDS文件,函数createfn.gds(), add.gdsn(), put.attr.gdsn(), write.gdsn() 和 index.gdsn() 都在gdsfmt包中定义。这部分具体示例代码可以联系小师妹哦~
- 从其他文件转换格式
SNPRelate包提供了snpgdsPED2GDS()和snpgdsBED2GDS()函数,用于将PLINK文本/二进制文件转换为GDS文件:
# PLINK BED文件,使用SNPRelate包中的例子
bed.fn <- system.file(“extdata”, “plinkhapmap.bed.gz”, package=”SNPRelate”)
fam.fn <- system.file(“extdata”, “plinkhapmap.fam.gz”, package=”SNPRelate”)
bim.fn <- system.file(“extdata”, “plinkhapmap.bim.gz”, package=”SNPRelate”)
或者,也可以使用你自己的PLINK文件:
bed.fn <- “C:/your_folder/your_plink_file.bed”
fam.fn <- “C:/your_folder/your_plink_file.fam”
bim.fn <- “C:/your_folder/your_plink_file.bim”
最后,使用snpgdsBED2GDS进行一步转换:
# 转换
snpgdsBED2GDS(bed.fn, fam.fn, bim.fn, “test.gds”)
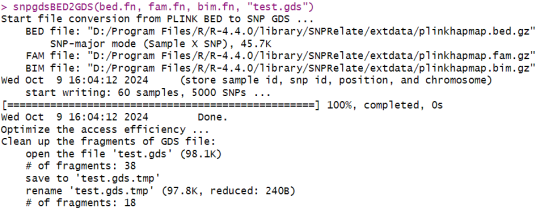
snpgdsSummary(“test.gds”)

另外,对于VCF文件的转换,除了可以用SNPRelate包提供的snpgdsVCF2GDS()函数,还能用SeqArray包里的seqVCF2GDS()函数来搞定,而且它还能一次性处理好几个VCF文件。这个函数会默认把数据压缩起来,省空间又高效。如果你在研究全基因组测序数据,那SeqArray包绝对是你的好帮手。想要了解更多细节,欢迎联系小师妹哦~
二、 数据分析
接下来,跟着小师妹一起探索如何利用这个强大的工具进行数据分析,包括基于LD的SNP修剪、主成分分析(PCA)、Fst估计和亲缘关系分析。准备好了吗?让我们开始吧!
- 基于LD的SNP修剪
LD,或称连锁不平衡,描述的是某些基因型在一起出现频率较高的现象。当我们准备进行主成分分析(PCA)之前,通常要先对SNPs进行LD修剪。经过修剪后,这些SNP之间大致处于连锁平衡,可以避免在主成分分析和亲缘关系分析中SNP簇的强影响。
set.seed(1000)
# 打开GDS文件
genofile <- snpgdsOpen(snpgdsExampleFileName())
# 可以尝试不同的LD阈值进行分析
snpset <- snpgdsLDpruning(genofile, ld.threshold=0.2)
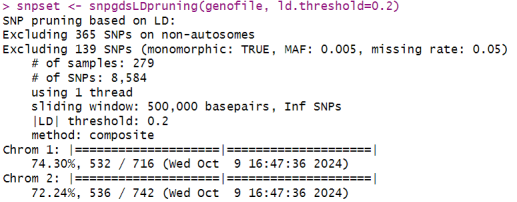
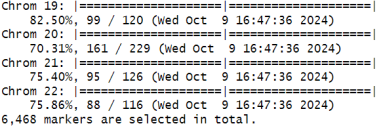
str(snpset)

names(snpset)
# 获取所有选择的 snp id
snpset.id <- unlist(unname(snpset))
head(snpset.id)

- 主成分分析(PCA)
SNPRelate中的PCA函数包括从基因型计算遗传协方差矩阵、计算样本载荷与每个SNP基因型之间的相关系数、计算SNP特征向量(载荷),以及从指定的SNP特征向量估计新数据集的样本载荷。
# 运行PCA
pca <- snpgdsPCA(genofile, snp.id=snpset.id, num.thread=2)

下面的代码展示了如何计算前几个主成分所占的变异百分比。可以明显看出,前两个特征向量在总体变异中占据了最大的比例,尽管总变异仍然不足四分之一。
# 变异比例(%)
pc.percent <- pca$varprop * 100
head(round(pc.percent, 2))

如果没有先前的人口信息,我们可以创建一个数据框:
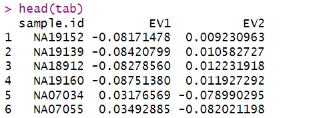
# 创建数据框
tab <- data.frame(sample.id = pca$sample.id,
EV1 = pca$eigenvect[,1], # 第一个特征向量
EV2 = pca$eigenvect[,2], # 第二个特征向量
stringsAsFactors = FALSE)
head(tab)
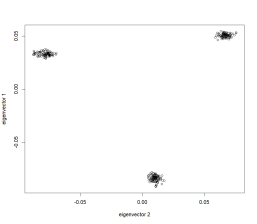
然后我们可以绘制这两个特征向量的散点图:
# 绘图
plot(tab$EV2, tab$EV1, xlab=”eigenvector 2″, ylab=”eigenvector 1″)
如果有人口信息,我们可以这样处理:
# 获取样本ID
sample.id <- read.gdsn(index.gdsn(genofile, “sample.id”))
# 获取人口信息
pop_code <- read.gdsn(index.gdsn(genofile, “sample.annot/pop.group”))
# 假设样本ID的顺序与人口代码相同
head(cbind(sample.id, pop_code))
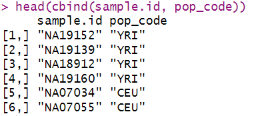
创建一个包含人口信息的数据框:
# 创建数据框
tab <- data.frame(sample.id = pca$sample.id,
pop = factor(pop_code)[match(pca$sample.id, sample.id)],
EV1 = pca$eigenvect[,1], # 第一个特征向量
EV2 = pca$eigenvect[,2], # 第二个特征向量
stringsAsFactors = FALSE)
head(tab)

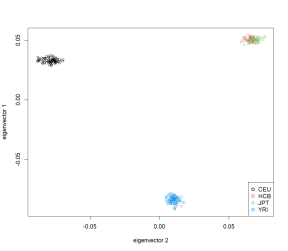
接下来,我们可以绘制不同人口群体的散点图:
# 绘图
plot(tab$EV2, tab$EV1, col=as.integer(tab$pop), xlab=”eigenvector 2″, ylab=”eigenvector 1″)
legend(“bottomright”, legend=levels(tab$pop), pch=”o”, col=1:nlevels(tab$pop))
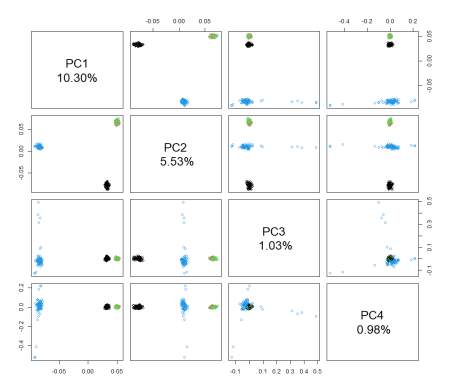
绘制前四个主成分的成对图:
lbls <- paste(“PC”, 1:4, “\n”, format(pc.percent[1:4], digits=2), “%”, sep=””)
pairs(pca$eigenvect[,1:4], col=tab$pop, labels=lbls)
对于前几个主成分的平行坐标图:
library(MASS)
datpop <- factor(pop_code)[match(pca$sample.id, sample.id)]
parcoord(pca$eigenvect[,1:16], col=datpop)

要计算特征向量与SNP基因型之间的相关性:
# 获取染色体索引
chr <- read.gdsn(index.gdsn(genofile, “snp.chromosome”))
CORR <- snpgdsPCACorr(pca, genofile, eig.which=1:4)
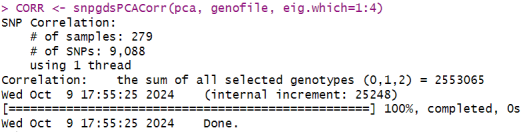
savepar <- par(mfrow=c(2,1), mai=c(0.45, 0.55, 0.1, 0.25))
for (i in 1:2)
{plot(abs(CORR$snpcorr[i,]), ylim=c(0,1), xlab=””, ylab=paste(“PC”, i),
col=chr, pch=”+”)}
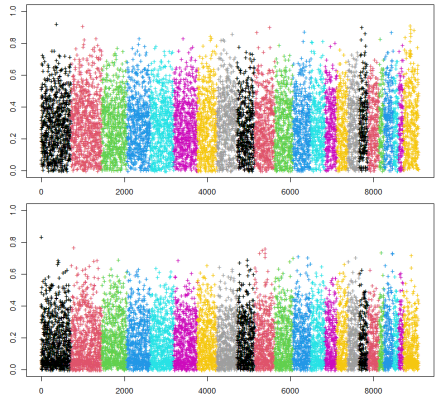
par(savepar)
- Fst估计
Fst,即固定指数,是衡量种群间遗传分化的一个经典指标。通过Fst估计,我们可以了解不同群体间的遗传差异。在拥有两个或更多种群的情况下,我们可以使用Weir和Cockerham(1984)的方法来估计Fst。
# 获取样本ID
sample.id <- read.gdsn(index.gdsn(genofile, “sample.id”))
# 获取种群信息
pop_code <- read.gdsn(index.gdsn(genofile, “sample.annot/pop.group”))
# 选择两个种群:HCB和JPT
flag <- pop_code %in% c(“HCB”, “JPT”)
samp.sel <- sample.id[flag]
pop.sel <- pop_code[flag]
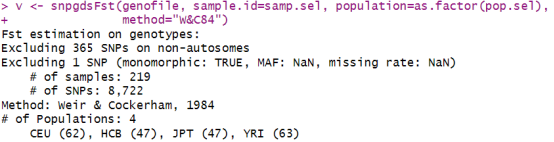
v <- snpgdsFst(genofile, sample.id=samp.sel, population=as.factor(pop.sel), method=”W&C84″)
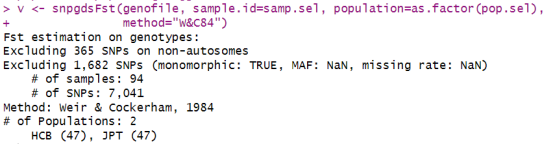
v$Fst # Weir和Cockerham加权Fst估计

v$MeanFst # Weir和Cockerham平均Fst估计
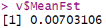
summary(v$FstSNP)
如果我们想要对多个种群进行Fst估计,比如CEU、HCB、JPT和YRI,我们需要先排除后代。
# 排除后代
father <- read.gdsn(index.gdsn(genofile, “sample.annot/father.id”))
mother <- read.gdsn(index.gdsn(genofile, “sample.annot/mother.id”))
flag <- (father==””) & (mother==””)
samp.sel <- sample.id[flag]
pop.sel <- pop_code[flag]
v <- snpgdsFst(genofile, sample.id=samp.sel, population=as.factor(pop.sel), method=”W&C84″)
v$Fst # Weir和Cockerham加权Fst估计
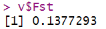
v$MeanFst # Weir和Cockerham平均Fst估计

summary(v$FstSNP)

- 亲缘关系分析
在亲缘关系分析中,SNPRelate中可以使用矩估计(Method of Moments,MoM)方法或最大似然估计(MLE)来进行基于血缘同源(IBD)的亲缘关系分析。对于这两种方法,建议使用连锁不平衡修剪后的SNP集合哦~
(1)使用PLINK方法的矩估计(MoM)估算IBD
# 获取样本ID
sample.id <- read.gdsn(index.gdsn(genofile, “sample.id”))
# 筛选YRI人群的样本ID
YRI.id <- sample.id[pop_code == “YRI”]
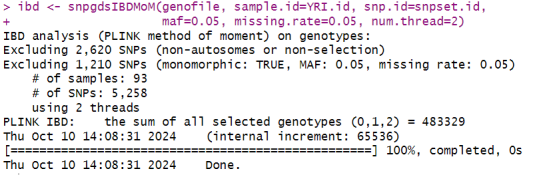
# 估算IBD系数
ibd <- snpgdsIBDMoM(genofile, sample.id=YRI.id, snp.id=snpset.id,
maf=0.05, missing.rate=0.05, num.thread=2)
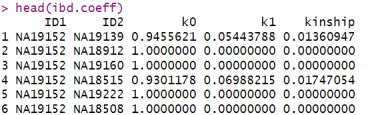
# 构建数据框
ibd.coeff <- snpgdsIBDSelection(ibd)
head(ibd.coeff)
# 绘制散点图
plot(ibd.coeff$k0, ibd.coeff$k1, xlim=c(0,1), ylim=c(0,1),
xlab=”k0″, ylab=”k1″, main=”YRI样本 (MoM)”)
lines(c(0,1), c(1,0), col=”red”, lty=2)
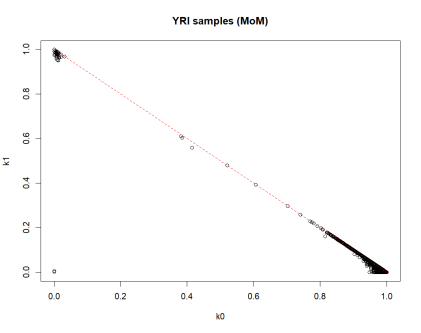
图里的每个点都代表一对个体,横轴k0表示他们没共享基因的概率,纵轴k1表示共享了一个基因的概率。如果两个个体没啥亲缘关系,点会靠在图的右下角;如果是亲兄弟,点会靠在左上角。那条红色的虚线表示k0和k1相等,也就是共享和不共享基因的概率差不多。如果点离这条线远,尤其是远离右下角,那可能说明个体间有较近的亲缘关系哦!
(2)使用最大似然估计(MLE)估算IBD系数
除了前面提到的PLINK方法的矩估计(MoM),我们还可以使用最大似然估计(MLE)来更精确地进行这一估算。最大似然估计(MLE)是一种统计方法,它通过寻找能够使观测数据出现概率(似然函数)最大化的参数值来进行参数估计。在遗传学中,MLE被广泛用于估算遗传参数,包括IBD。
首先,我们需要从大量的单核苷酸多态性(SNP)中随机选择一部分来进行分析。这样做可以减少计算量,同时仍然能够获得代表性的结果。在这个例子中,我们随机选择了1500个SNP。
# 设置随机数种子,以确保结果的可重复性
set.seed(100)
# 从选定的SNP集合中随机选择1500个SNP
snp.id <- sample(snpset.id, 1500)
接下来,我们使用snpgdsIBDMLE函数来进行IBD的估算。这个函数接受基因文件、样本ID、SNP ID等参数,并返回每对个体之间的IBD估计值。
# 使用MLE方法估算IBD
ibd <- snpgdsIBDMLE(genofile, sample.id=YRI.id, snp.id=snp.id,
maf=0.05, missing.rate=0.05, num.thread=2)
在这段代码中,我们指定了最小等位基因频率(MAF)为0.05,缺失率为0.05,并使用2个线程来加速计算。函数会返回一个包含IBD估计值的对象。
最后,我们可以使用snpgdsIBDSelection函数来提取IBD系数,并将其存储在一个数据框中。
# 提取IBD系数
ibd.coeff <- snpgdsIBDSelection(ibd)
# 绘制散点图
plot(ibd.coeff$k0, ibd.coeff$k1, xlim=c(0,1), ylim=c(0,1),
xlab=”k0″, ylab=”k1″, main=”YRI样本 (MLE)”)
lines(c(0,1), c(1,0), col=”red”, lty=2)
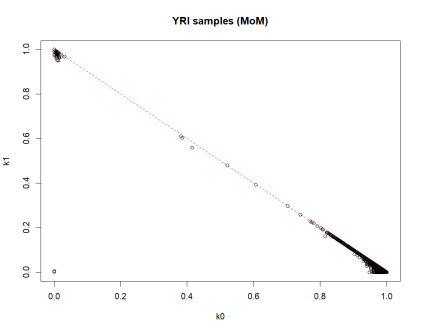
(3)使用KING方法的矩估计推断亲缘关系
在遗传学研究中,我们经常需要推断个体之间的亲缘关系,尤其是在存在人群分层的情况下。KING方法是一种在这种情况下非常有效的工具,它可以在家族内和家族间推断亲缘关系,并且对人群分层具有鲁棒性。
首先,我们需要获取家族信息,这可以通过读取GDS文件中的家族ID来实现。在这个例子中,我们选择了YRI样本的家族ID。
# 读取家族ID
family.id <- read.gdsn(index.gdsn(genofile, “sample.annot/family.id”))
# 根据YRI样本的ID筛选对应的家族ID
family.id <- family.id[match(YRI.id, sample.id)]
# 查看家族ID的分布情况
table(family.id)

接下来,我们使用snpgdsIBDKING函数来进行亲缘关系的推断。这个函数接受基因文件、样本ID、家族ID等参数,并返回每对个体之间的亲缘关系估计值。
# 使用KING方法推断亲缘关系
ibd.robust <- snpgdsIBDKING(genofile, sample.id=YRI.id,
family.id=family.id, num.thread=2)

最后,我们可以使用snpgdsIBDSelection函数来提取亲缘关系估计值,并将其存储在一个数据框中。
# 提取亲缘关系估计值
dat <- snpgdsIBDSelection(ibd.robust)
# 绘制散点图
plot(dat$IBS0, dat$kinship, xlab=”Proportion of Zero IBS”,
ylab=”Estimated Kinship Coefficient (KING-robust)”)
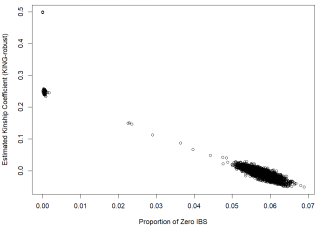
(4)状态同源(IBS)分析
IBS分析是一种衡量个体间基因型相似度的方法,它不考虑遗传差异的来源,只关注基因型是否相同。对于n个研究个体,我们可以使用snpgdsIBS()函数来创建一个n×n的矩阵,其中包含了全基因组平均IBS配对身份。
# 进行IBS分析
ibs <- snpgdsIBS(genofile, num.thread=2)
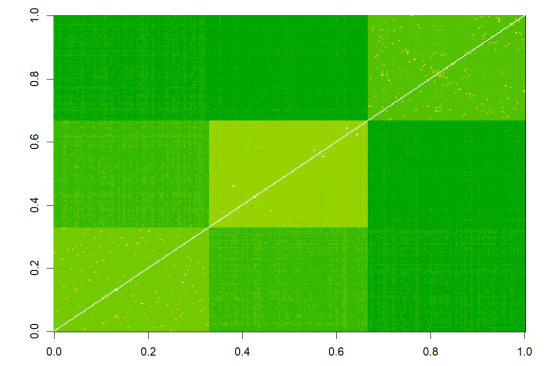
这段代码会排除非常染色体上的SNP,并计算所有选定基因型(0,1,2)的总和。分析完成后,我们可以通过热图来直观地展示结果:
# 将同一人群中的个体聚集在一起
pop.idx <- order(pop_code)
# 展示热图
image(ibs$ibs[pop.idx, pop.idx], col=terrain.colors(16))
接下来,我们可以使用多维尺度分析(MDS)来分析全基因组IBS配对距离的n×n矩阵:
# 进行MDS分析
loc <- cmdscale(1 – ibs$ibs, k = 2)
x <- loc[, 1]; y <- loc[, 2]
race <- as.factor(pop_code)
# 绘制MDS图
plot(x, y, col=race, xlab = “”, ylab = “”,
main = “Multidimensional Scaling Analysis (IBS)”)
legend(“topleft”, legend=levels(race), pch=”o”, text.col=1:nlevels(race))

此外,我们还可以进行聚类分析,以确定个体的群体,并通过置换分数自动确定群体:
# 设置随机数种子
set.seed(100)
# 进行聚类分析
ibs.hc <- snpgdsHCluster(snpgdsIBS(genofile, num.thread=2))
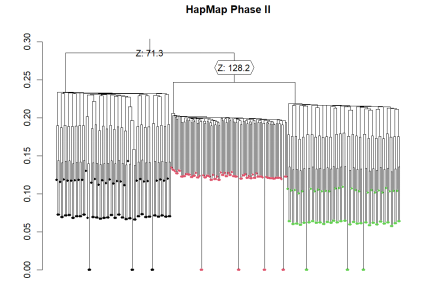
然后,我们可以通过绘制树状图来确定个体的群体:
# 自动确定个体的群体
rv <- snpgdsCutTree(ibs.hc)
# 绘制树状图
plot(rv$dendrogram, leaflab=”none”, main=”HapMap Phase II”)
我们还可以基于已知的人口信息来确定个体的群体:
# 根据人口信息确定个体的群体
rv2 <- snpgdsCutTree(ibs.hc, samp.group=as.factor(pop_code))
# 绘制树状图
plot(rv2$dendrogram, leaflab=”none”, main=”HapMap Phase II”)
legend(“topright”, legend=levels(race), col=1:nlevels(race), pch=19, ncol=4)

最后,别忘了关闭GDS文件:
snpgdsClose(genofile)
通过这些分析,我们可以更好地理解个体之间的遗传关系,这对于遗传学研究和人群遗传结构分析都是非常有帮助的。如果你对这个过程还有任何疑问,或者需要进一步的帮助,随时可以联系小师妹哦!
无论你是在优化代码,还是在云端进行便捷的分析,云生信神器都能为你提供强大的支持。欢迎试试我们的云生信神器,只需一键上传数据,想要的图就能轻松get~