嘿朋友们,欢迎来到生物信息学的精彩世界!今天,小果将带领大家一起学习R包Omada,这是一款无监督机器学习工具,它能够自动对基因表达谱进行样本聚类,为我们揭示复杂疾病中分子状态的差异。
在RNA分析研究中,探索性聚类分析需要对众多参数进行选择,这要求对机器学习有深入了解并进行大量的计算实验。Omada通过自动化的机器学习功能,使得无监督聚类转录组数据更加方便快捷。即使在生物学区分不太明显的数据集中,它也能帮助我们找到具有不同表达谱和临床关联的稳定亚组。注意哦,GLAD包操作占用内存比较大,建议使用服务器哦,欢迎联系小果租赁性价比高的服务器~
下面,小果将引领大家逐步掌握操作流程,从分析数据集的聚类可行性开始,到选择最优聚类方法,再到选择最优特征,估计最优聚类数量,最后运行最优聚类,我们将一同穿越基因表达谱的聚类迷宫。如果你在旅途中遇到任何困难,别担心,小果随时待命,记得联系小果为你解答疑惑~
我们先安装并加载omada包:
if (!require(“BiocManager”, quietly = TRUE))
install.packages(“BiocManager”)
BiocManager::install(“omada”)
library(omada)
- 数据集的聚类可行性
第一步,我们需要根据数据集的维度(样本和特征大小)调查其聚类的可行性。为了研究数据集的聚类可行性,omada包提供了两个稳定性评估模拟函数,它们模拟特定维度的数据集并计算一系列聚类的数据集稳定性。
第一个函数是feasibilityAnalysis() ,它为特定数量的类、样本和特征生成一个独立数据集,该数据集包含了4个类别(classes)、50个样本(samples)和15个特征(features)。
# Selecting dimensions and number of clusters
new.dataset.analysis <- feasibilityAnalysis(classes = 4, samples = 50, features = 15)
第二个函数是feasibilityAnalysisDataBased(),它接受现有数据集,提取特定数量聚类的统计数据(平均值和标准差),该数据集基于toy_genes数据集,包含了3个类别。
# Basing the simulation on an existing dataset and selecting the number of clusters
existing.dataset.analysis <- feasibilityAnalysisDataBased(data = toy_genes, classes = 3)
接着,调用以下函数来提取这两种分析方法的结果:
- get_average_stabilities_per_k:获取每个聚类数k的平均稳定性
- get_max_stability:获取新数据集分析对象的最大稳定性
- get_average_stability:获取新数据集分析对象的平均稳定性
- get_generated_dataset:获取新数据集分析对象生成的数据集
# Extract results of either function
average.sts.k <- get_average_stabilities_per_k(new.dataset.analysis) #
maximum.st <- get_max_stability(new.dataset.analysis)
average.st <- get_average_stability(new.dataset.analysis)
generated.ds <- get_generated_dataset(new.dataset.analysis)

请注意,这些估计值仅作为数据集是否适合聚类的指示,而不是质量的实际衡量标准,因为它们不考虑数据中的实际信号,而只考虑样本、特征和聚类数量之间的关系。
二、自动聚类分析
接下来,我们就可以使用 omada()来运行整个分析工具包,自动化聚类决策并生成估计的最佳簇。 omada()的输入是基因表达数据框和要考虑的簇数上限 k。小果提醒大家,在运行任何工具之前,都不要忘了提前删除或估算 NA 值哦。
# Running the whole cascade of tools inputting an expression dataset
# and the upper k (number of clusters) to be investigated
omada.analysis <- omada(toy_genes, method.upper.k = 6)
接着,我们可以利用各种函数提取得到下列这些分析结果,例如特征选择分数(fs.scores)、最佳特征选择结果(fs.optimal.features)、聚类投票分数(cv.scores)、样本的成员关系(sample.memberships)等等。
# Extract results
pa.scores <- get_partition_agreement_scores(omada.analysis)
fs.scores <- get_feature_selection_scores(omada.analysis)
fs.optimal.features <- get_feature_selection_optimal_features(omada.analysis)
fs.optimal.number.of.features<-get_feature_selection_optimal_number_of_features(omada.analysis)
cv.scores <- get_cluster_voting_scores(omada.analysis)
cv.memberships <- get_cluster_voting_memberships(omada.analysis)
cv.metrics.votes <- get_cluster_voting_metric_votes(omada.analysis)
cv.k.votes <- get_cluster_voting_k_votes(omada.analysis)
sample.memberships <- get_sample_memberships(omada.analysis)
最后,我们可以绘制不同的结果图,如分区协议图、特征选择图、聚类投票图等,帮助我们更好地理解数据集的结构、特征选择情况以及聚类结果,为进一步的数据分析和解释提供重要参考。
# Plot results
plot_partition_agreement(omada.analysis)
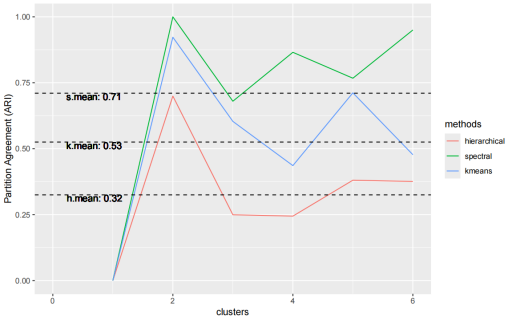
分区一致性图显示了在不同聚类数(k值)下,数据集内部的分区一致性和稳定性。x轴代表聚类数(k值),y轴代表分区一致性得分(Partition Agreement Score)。随着聚类数的增加,分区一致性分数会变化,通常在一个较高的分区一致性得分附近选择最佳的聚类数(最佳k值)。这个图可以帮助确定数据集在哪个聚类数下表现最佳,以选择合适的聚类数用于进一步分析和解释。
plot_feature_selection(omada.analysis)

特征选择图展示了在不同特征选择数量下,特征选择效果的比较。这个图可以帮助识别哪种特征选择方法在数据集中表现最佳,有助于提高后续分析的准确性和效果。
plot_cluster_voting(omada.analysis)
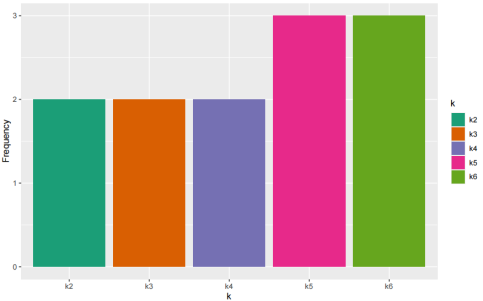
聚类投票图展示了聚类方法的得分柱状图,显示了不同聚类方法的得分,可参考各聚类方法在数据集上的表现。
三、选择最优聚类方法
第三步,我们可以根据数据集选择最合适的聚类方法。使用 clusteringMethodSelection() 函数比较三种不同方法(即谱聚类、k 均值聚类、层次聚类)的内部分区一致性。我们可以定义上限 k 以及每种方法的内部比较次数。比较次数的增加会带来更高的稳健性和最高的运行时间。
# Selecting the upper k limit and number of comparisons
method.results <- clusteringMethodSelection(toy_genes, method.upper.k = 3, number.of.comparisons = 2)
# Extract results
pa.scores <- get_partition_agreement_scores(method.results)
# Plot results
plot_partition_agreement(method.results)
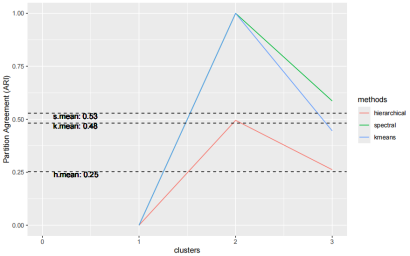
分析上图,我们可以发现,使用谱聚类(绿色线)的分区一致性得分最高(k_maen=0.53),因此在后续的步骤中,我们可以指定使用谱聚类的方法。
Omada包还提供了通过利用函数partitionAgreement()单独计算两个特定聚类方法和参数集之间的分区一致性的函数,该函数需要选择两种算法、度量和聚类数量。
# Selecting algorithms, measures and number of clusters
agreement.results <- partitionAgreement(toy_genes, algorithm.1 = “spectral”, measure.1 = “rbfdot”, algorithm.2 = “kmeans”,measure.2 = “Lloyd”, number.of.clusters = 3)
# Extract results
pa.scores <- get_agreement_scores(agreement.results)
四、选择最优特征
为了选择提供最稳定聚类的特征,函数 featureSelection() 需要最小和最大聚类数 (k) 以及决定每个特征集增加率的特征步骤。在本例中,我们选择了最小聚类数为3,最大聚类数为6,并设置了每个特征集增加率的特征步骤为3。
# Selecting minimum and maximum number of clusters and feature step
feature.selection.results <- featureSelection(toy_genes, min.k = 3, max.k = 6, step = 3)
从结果中提取平均特征稳定性得分,最佳特征数以及最佳特征集。平均特征稳定性得分可以帮助评估不同特征集的稳定性,最佳特征数则指示了在给定聚类范围内所选择的最佳特征数量。
# Extract results
feature.selection.scores <- get_average_feature_k_stabilities(feature.selection.results)
optimal.number.of.features <- get_optimal_number_of_features
optimal.features <- get_optimal_features(feature.selection.results)
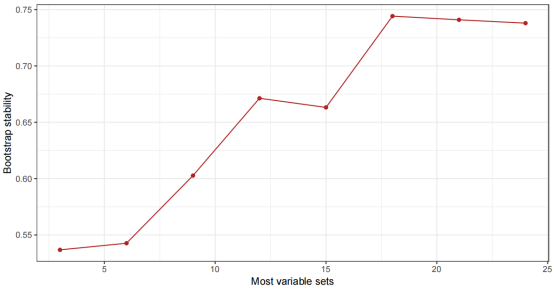
通过绘制平均稳定性结果图,可以直观地观察不同特征数量下的稳定性得分趋势,从而更好地理解哪些特征数量组合提供了最稳定的聚类结果。
# Plot results
plot_average_stabilities(feature.selection.results)
五、估计最优聚类数量
通过使用clusterVoting()函数,我们可以根据内部指标集合估计最合适的聚类数,并选择要考虑的最小和最大聚类数以及所选算法(“sc” 表示谱聚类,“km” 表示k 均值聚类,“hr” 表示层次聚类)进行聚类投票。在本例中,我们选择将最小聚类数设为4,最大聚类数设为8,并选择谱聚类算法进行聚类投票。
# Selecting minimum and maximum number of clusters and algorithm to be used
cluster.voting.results <- clusterVoting(toy_genes, 4,8,”sc”)
从结果中提取内部指标得分、聚类成员关系以及投票频率等相关指标数据,并利用这些数据来评估不同聚类数下的内部指标表现及最合适的聚类数。
# Extract results
internal.metric.scores <- get_internal_metric_scores(cluster.voting.results)
cluster.memberships.k <- get_cluster_memberships_k(cluster.voting.results)
metric.votes.k <- get_metric_votes_k(cluster.voting.results)
vote.frequencies.k <- get_vote_frequencies_k(cluster.voting.results)
通过绘制投票频率结果图,可以直观地展示在考虑不同聚类数和所选算法的情况下各个内部指标得出的投票频率,帮助我们理解哪个聚类数最受内部指标的支持。
# Plot results
plot_vote_frequencies(cluster.voting.results)
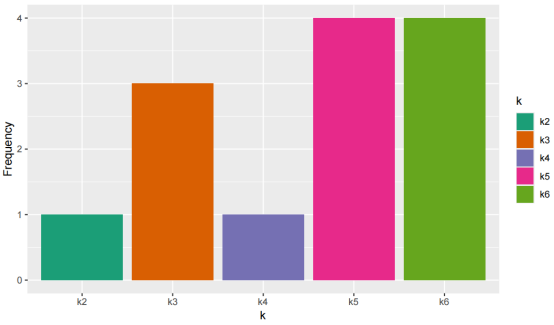
- 运行最优聚类
最后,我们可以基于上面获得的最优的参数,使用optimalClustering() 来运行最优聚类啦!这个函数还会自动运行可能的算法参数,保留稳定性最高的算法参数。
# Running the clustering with specific number of clusters(k) and algorithm
sample.memberships <- optimalClustering(toy_genes, 4, “spectral”)
# Extract results
memberships <- get_optimal_memberships(sample.memberships)
optimal.stability <- get_optimal_stability_score(sample.memberships)
optimal.parameter <- get_optimal_parameter_used(sample.memberships)

最终,我们可以提取最优的结果:最优的聚类结果存储在memberships中,可以对聚类结果进行进一步分析和可视化。最优的稳定性分数为0.715,表明聚类结果的稳定性较高。使用了最优的算法参数rbfdot,这表明在这个参数设置下得到了最优的聚类结果。
综合以上结果,我们得到了稳定且高效的最优聚类结果,可用于后续的数据分析和挖掘。
怎么样,AI的世界是不是很神奇?好啦,小果已经带领大家一起完成了Omada包的初步探索,你有没有对AI在基因表达谱的聚类上的应用有了感性的认识呢?现在,你可以开始展开自己的实践,利用omada包来构建属于你自己的模型啦!
无论你是在优化代码,还是在云端进行便捷的分析,云生信神器都能为你提供强大的支持。欢迎试试我们的云生信神器,只需一键上传数据,想要的图就能轻松get~