嗨,探索者们,小果向导再次欢迎你们!今天,我们的探险目的地是神秘而又复杂的微生物组世界。在这个世界里,每一个微生物都扮演着其独特的角色,而它们之间错综复杂的相互作用构成了一个庞大的网络。为了更好地理解这个网络,我们需要一把强大的工具——那就是DirichletMultinomial包。
微生物组数据,充满了未知和挑战,但同时也蕴藏着无限的可能性。通过分析这些数据,我们可以揭示微生物多样性的秘密,理解它们在环境和宿主健康中的作用。DirichletMultinomial包,就是我们在这场探险中的神器。它利用机器学习构建了Dirichlet多项式分布模型来分析微生物组数据,帮助我们识别出微生物群落中的模式和趋势。
使用DirichletMultinomial包,我们可以轻松处理大规模的微生物组数据,从而预测微生物的丰度分布,探索微生物群落的结构变化,甚至是它们对环境变化的响应。记住,这个包需要较大的计算资源,因此建议在服务器上进行计算,小果这里有性价比超高的服务器推荐哦~
现在,让小果带领大家一步步深入微生物组数据的分析过程,从数据准备到深度解析,我们将一同探索微生物多样性的奥秘。在这个旅程中遇到任何问题,都不要犹豫,小果随时在这里为你提供帮助~
我们先安装并加载DirichletMultinomial包,此外还有 lattice 包(用于可视化)和 parallel 包(用于在交叉验证期间使用多个核心)。
if (!require(“BiocManager”, quietly = TRUE))
install.packages(“BiocManager”)
BiocManager::install(“DirichletMultinomial”)
library(DirichletMultinomial)
library(lattice)
library(xtable)
library(parallel)
接着,我们进行一些基本的设置,例如将在R中设置输出宽度,修改浮点数的显示精度,在可视化时采用`.qualitative`等等。
options(width=70, digits=2)
full <- FALSE
.qualitative <- DirichletMultinomial:::.qualitative
dev.off <- function(…) invisible(grDevices::dev.off(…))
接下来,让我们步入正题,开始我们的微生物组数据分析之旅~ 整个旅程可以分成三步:数据、聚类和生成分类器。
- 数据
第一步,获取数据。我们可以读取DirichletMultinomial包中的数据文件’Twins.csv’,然后将数据转换为样本×物种的计数矩阵。数据包含了关于样本和物种(微生物)的计数信息,这些计数数据通常来自于微生物组学研究中的测序数据,用于分析不同样本中微生物的存在和丰度。
fl <- system.file(package=”DirichletMultinomial”, “extdata”,
“Twins.csv”)
count <- t(as.matrix(read.csv(fl, row.names=1)))
count[1:5, 1:3]

在count的输出里我们可以看到,列名表示不同的微生物,行名代表不同的样本,counts则表示各种微生物在各样本里的计数。
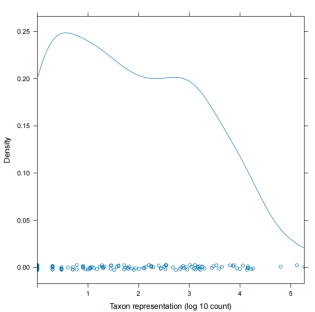
接着,我们可以生成一个展示微生物组数据中各微生物相对丰度(经过对数转换)的密度图。横轴表示了微生物的表示量(以log10计数表示),纵轴表示了密度。这种图形有助于我们理解数据的整体分布,特别是在对数尺度上,可以更清晰地看到哪些微生物的丰度较高或较低,以及丰度分布的形状(如是否呈现正态分布、是否有长尾等)。
cnts <- log10(colSums(count))
pdf(“taxon-counts.pdf”)
densityplot(cnts, xlim=range(cnts),
xlab=”Taxon representation (log 10 count)”)
dev.off()
- 聚类
第二步,我们可以开始聚类。`dmn`函数可以用于拟合Dirichlet-Multinomial模型,它的输入是counts数据和参数k(代表要建模的Dirichlet成分数量)。我们可以选取不同的k值(1~7)进行拟合(1~7),在这里我们只展示k=4的结果。
if (full) {
fit <- mclapply(1:7, dmn, count=count, verbose=TRUE)
save(fit, file=file.path(tempdir(), “fit.rda”))
} else data(fit)
fit[[4]]
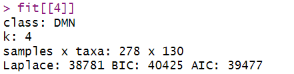
在k=4的结果输出中,Laplace: 38781,BIC: 40425,AIC: 39477 分别是该模型的拉普拉斯近似值、贝叶斯信息准则(BIC)和 赤池信息准则(AIC),可以作为模型选择的评价指标。
我们可以绘制不同 Dirichlet 成分数量下模型拟合度的折线图,分析图我们可以发现最佳拟合是k = 4 个不同的狄利克雷成分。
lplc <- sapply(fit, laplace)
pdf(“min-laplace.pdf”)
plot(lplc, type=”b”, xlab=”Number of Dirichlet Components”,
ylab=”Model Fit”)
dev.off()
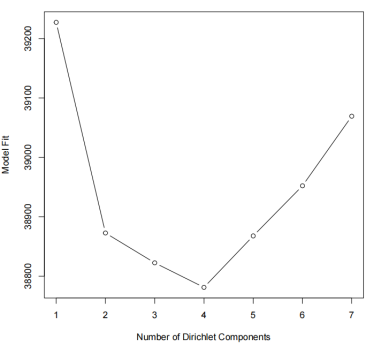
接着,我们可以从中选择出拟合效果最佳的模型存储在 best 变量中。然后,我们就可以从best对象中提取特定的信息。mixturewt 函数报告拟合模型的权重 pi 和同质性 theta(值越大越同质)。mixture 返回样本 x 估计的狄利克雷成分的矩阵;参数assign 返回一个长度等于样本数量的向量,表示具有最大值的成分。
(best <- fit[[which.min(lplc)]])
mixturewt(best)
head(mixture(best), 3)
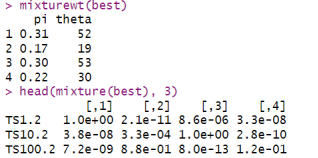
Fitted函数可以描述每个分类群(下图每格中的每个点)对狄利克雷成分的贡献;图中点的对角线表明狄利克雷成分是具有相关性的,可能反映了整体的数值丰度。

我们可以计算最佳和单成分狄利克雷多项式模型之间的后验均值差异,它可以衡量每个成分与总体平均值的差异;而总和则是与平均值的总差异的衡量标准。
p0 <- fitted(fit[[1]], scale=TRUE) # scale by theta
p4 <- fitted(best, scale=TRUE)
colnames(p4) <- paste(“m”, 1:4, sep=””)
(meandiff <- colSums(abs(p4 – as.vector(p0))))
sum(meandiff)

我们可以计算两个拟合模型之间每行的绝对差异之和,得到一个包含各种微生物的向量。经处理可以得到一个数据框,包括每种微生物在两个模型中的拟合值、差异值和累积差异比率,总结了对每个狄利克雷成分的分类贡献。
diff <- rowSums(abs(p4 – as.vector(p0)))
o <- order(diff, decreasing=TRUE) #对差异向量进行降序排序
cdiff <- cumsum(diff[o]) / sum(diff) #计算累积差异比率,即累积差异之和除以总差异之和
df <- head(cbind(Mean=p0[o], p4[o,], diff=diff[o], cdiff), 10)
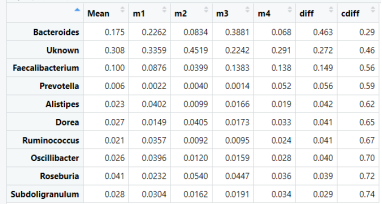
我们也可以使用xtable函数将数据框df转换为一个格式化的表格,并设置表格的标题、标签、对齐方式等属性。然后通过print函数打印出这个表格。
xtbl <- xtable(df,
caption=”Taxonomic contributions (10 largest) to Dirichlet components.”,
label=”tab:meandiff”, align=”lccccccc”)
print(xtbl, hline.after=0, caption.placement=”top”)
下图可以展示微生物按照狄利克雷成分排列的情况,每个样本被放入具有最大拟合值的成分中。通过以下代码将图表保存为名为”heatmap1.pdf”的PDF文件:
pdf(“heatmap1.pdf”)
heatmapdmn(count, fit[[1]], best, 30)
dev.off()
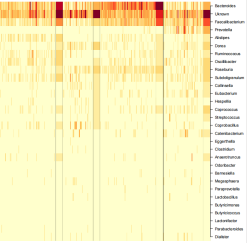
在图中,窄列表示微生物,宽列表示成分的平均值。每行对应一个分类组。颜色编码代表平方根计数,深色表示较大的计数。这幅图可帮助观察样本在不同狄利克雷成分下的分布情况,并展示了计数值的相对大小。
- 生成分类器
我们可以使用以下代码读取每个样本的表型信息,将表型信息进行因子化处理(’Lean’,’Obese’,’Overweight’),再将表型信息与数据矩阵中的行名称进行匹配,并使用table(pheno)对表型进行计数,并输出结果。输出表明有61个样本被归类为’Lean’,193个样本为’Obese’,24个样本为’Overwt’。这有助于了解样本中不同表型的分布情况。
fl <- system.file(package=”DirichletMultinomial”, “extdata”,
“TwinStudy.t”)
pheno0 <- scan(fl)
lvls <- c(“Lean”, “Obese”, “Overwt”)
pheno <- factor(lvls[pheno0 + 1], levels=lvls)
names(pheno) <- rownames(count)
table(pheno)

这里我们将数据按表型分成子计数,每个表型一个子计数。每个子计数显示了对应表型的样本数。
counts <- lapply(levels(pheno), csubset, count, pheno)
sapply(counts, dim)
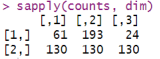
接着,需要对表型信息进行相应更新,只保留’Lean’和’Obese’两种表型。
keep <- c(“Lean”, “Obese”)
count <- count[pheno %in% keep,]
pheno <- factor(pheno[pheno %in% keep], levels=keep)
接下来,小果带大家使用一个函数——dmngroup函数,它用于为每个组识别最佳(最小Laplace得分)的Dirichletmultinomial模型。
if (full) {
bestgrp <- dmngroup(count, pheno, k=1:5, verbose=TRUE,
mc.preschedule=FALSE)
save(bestgrp, file=file.path(tempdir(), “bestgrp.rda”))
} else data(bestgrp)
Lean组由一个成分模型描述,Obese组由一个包含三个成分的模型描述。原始单组(最佳)模型的四个Dirichle成分中,三个在Obese组中,另一个在Lean组中。两组模型的总Laplace分数比单组模型低,表明从单独考虑组别时获得了信息增益。
我们可以使用bestgrp查看最佳模型的摘要信息,包括每个组(Lean和Obese)的样本数量、物种数、负对数似然(NLE)、对数行列式(LogDet)、Laplace得分、贝叶斯信息准则(BIC)和赤池信息准则(AIC)等统计量。
bestgrp

对bestgrp中的每个组(Lean和Obese)应用mixturewt函数,可以显示每个组模型的成分权重(pi)和同质性(theta)。
lapply(bestgrp, mixturewt)
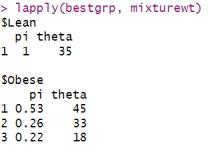
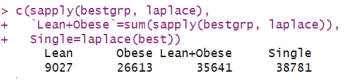
我们还可以计算各组(Lean和Obese)、整体组合(Lean+Obese)以及单一组模型的Laplace分数,结果表明Lean组和Obese组组合模型的总Laplace分数较低,这表明单一组模型获得了信息增益。
c(sapply(bestgrp, laplace),
`Lean+Obese`=sum(sapply(bestgrp, laplace)),
Single=laplace(best))
最后,我们要使用模型进行预测啦!使用predict函数可以将样本分配到不同的类别中。
xtabs(~pheno + predict(bestgrp, count, assign=TRUE))

在输出的矩阵中,行代表实际类别,列代表预测类别。输出值表示每个类别的样本数。在矩阵中,我们可以看到,对于实际为”Lean”的样本,有38个被正确地预测为”Lean”,23个被错误地预测为”Obese”。对于实际为”Obese”的样本,有178个被正确地预测为”Obese”,而有15个被错误地预测为”Lean”。显然,模型对于”Obese”的预测更加准确。
接下来,我们可以使用cvdmngroup 函数执行交叉验证,可以根据分组情况进行leave-one-out(LOO)交叉验证。注意哦,这是一个计算量很大的步骤,可能需要一点时间。
if (full) {
## full leave-one-out; expensive!
xval <- cvdmngroup(nrow(count), count, c(Lean=1, Obese=3), pheno,
verbose=TRUE, mc.preschedule=FALSE)
save(xval, file=file.path(tempdir(), “xval.rda”))
} else data(xval)
最后,我们就可以根据实际表型和预测结果分别生成针对单组/两组/整合分类器的ROC曲线。
bst <- roc(pheno[rownames(count)] == “Obese”,
predict(bestgrp, count)[,”Obese”])
bst$Label <- “Single”
two <- roc(pheno[rownames(xval)] == “Obese”,
xval[,”Obese”])
two$Label <- “Two group”
both <- rbind(bst, two)
pars <- list(superpose.line=list(col=.qualitative[1:2], lwd=2))
pdf(“roc.pdf”)
xyplot(TruePostive ~ FalsePositive, group=Label, both,
type=”l”, par.settings=pars,
auto.key=list(lines=TRUE, points=FALSE, x=.6, y=.1),
xlab=”False Positive”, ylab=”True Positive”)
dev.off()
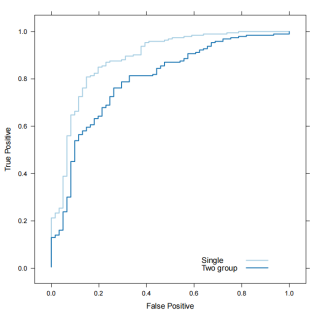
上图显示的ROC曲线图,展示了单组分类器和两组分类器的性能对比。其中,横轴为False Positive,纵轴为True Positive。通过ROC曲线对单组和两组分类器的性能进行了比较,结果显示单组分类器的表现优于两组分类器。
怎么样,AI的世界是不是很神奇?好啦,小果已经带领大家一起完成了DirichletMultinomial包的初步探索,你有没有对AI在分析微生物组数据上的应用有了感性的认识呢?现在,你可以开始自己动手,利用DirichletMultinomial包来构建属于你自己的模型啦!
无论你是在优化代码,还是在云端进行便捷的分析,云生信神器都能为你提供强大的支持。欢迎试试我们的云生信神器,只需一键上传数据,想要的图就能轻松get~